Applications Of Newton's First and Second Laws
Helena Dedic
Beware: Many of the solutions to these exercises use !
Exercise 1
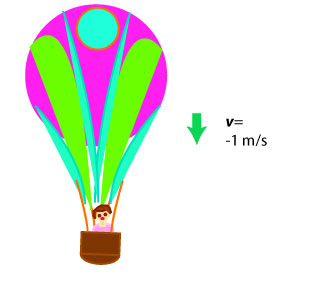
A 40 kg child is riding in a hot air balloon which is descending at a speed of 1 m/s. What is the normal force exerted on the child?
Exercise 2
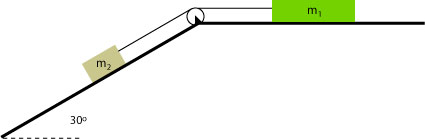
Two blocks, kg and kg, connected as shown in the diagram, move at constant velocity towards the left. Find the normal force on both blocks and the tension in the rope given that the force of friction on the block sliding horizontally is 15 N.
Exercise 3
Each block shown below has a mass of 10 kg. Find the magnitude and direction of the normal force acting on each block.

Exercise 4
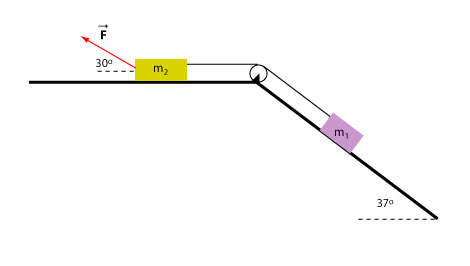
Two blocks, kg and kg are connected as shown in the diagram and moves at constant velocity up the incline because is pulled by a force F. Find the force F exerted on the block sliding along the horizontal towards the left, the normal force on both blocks and the tension in the rope given that the force of friction on both blocks is 20 N.
Exercise 5
Sally holds the two boxes, kg and kg at rest on the incline by pushing the blue box with a force F. Draw a free body diagram for each of the two boxes. Assume that there is no friction exerted on either of the two boxes. Determine the normal forces exerted on each of the boxes and the force exerted by Sally.
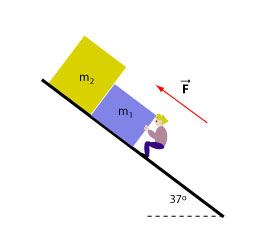
Exercise 6
A 20 kg child starts from rest and travels 3 m down a slide that is inclined 35° to the horizontal. If her speed at the bottom is 1 m/s, what was the frictional force along the slide?
Exercise 7
A man pushes a 20 kg lawn mover with a force of 80 N directed along the handle, which is inclined at to the horizontal.
(a) If he moves at constant velocity, what is the retarding force due to the ground?
(b) What force along the handle would produce an acceleration of 1 m/ given the same retarding force?
Exercise 8
A child drops from a ledge 1 m above the floor. Estimate the force on her 40 kg torso when she lands by bending her knees and stopping her torso in 30 cm or lands stiffly and her torso is stopped within 4 cm.
Exercise 9
Two blocks with masses kg and kg are connected by a light rope. The mass is placed on a frictionless incline that makes 30° with the horizontal. A force N acts on at 20° to the horizontal. Find the acceleration of the system and the tension in the rope.
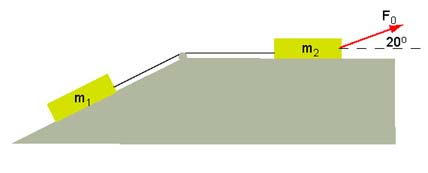
Exercise 10
Would it be easier to play catch with a large ball in the outer space since it has no weight?
Exercise 11
What is the reading on the spring scale for each of the situations depicted? Each block has a mass of 5 kg.
a)  b)
b) 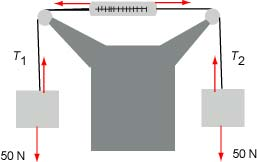 c)
c) 
Exercise 12
A ball thrown vertically upward momentarily comes to rest at its highest point. Is it in equilibrium at this instant? Explain why or why not.
Exercise 13
The 50 kg torso of a sprinter starts at rest and reaches 6 m/s within 80 cm, both measured horizontally. Estimate the acceleration and the horizontal force exerted on the torso-hip joint.
Exercise 14
A length of rope has a mass of 30 g. It is used to accelerate a 200 g object vertically upward at . What is the tension in the rope - at the bottom of the rope, at the top of the rope and in the middle of the rope?
Exercise 15
A block of mass 1 kg is on a frictionless incline and is subject to a horizontal force of 5 N. What is its acceleration? If it is initially moving up the incline at 4 m/s, what is its displacement along the incline in 2 s.
Exercise 16
A 3 kg block is suspended with two ropes, one of which is horizontal. Find the tension in each rope.
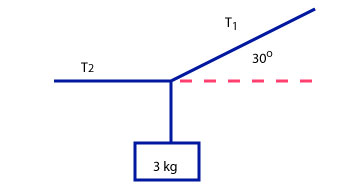
Exercise 17
A car is moving at 90 km/h. A 75-kg driver is held firmly in the seat by a seatbelt. Find the average force exerted on the driver by the seatbelt (in other words, assume that the force is constant) if the car crashes by crumpling through a distance of 75 cm.
Exercise 18
Two blocks with masses kg and kg hang under one another. Find the tensions in the (massless) ropes in the following situations:
(a) the blocks are at rest;
(b) they move upward at 5 m/s;
(c) they accelerate upward at 2 m/;
(d) they accelerate downward at 2 m/.
(e) if the maximum allowable tension in the rope is 10 N, what is the maximum possible upward acceleration?

Exercise 19
Two blocks are connected by a massless rope. The horizontal surface is frictionless. If kg for what value of will the
(a) acceleration of the system be 4 m/ or
(b) the tension in the rope be 8 N?

Exercise 20
A body experiences a force of 10 N directed at N of E and a force of 12.8 N directed at E of S. What third force would keep the body at equilibrium?
Exercise 21
What is the spring constant of a spring which stretches 1.5 cm when supporting a 2 kg mass on a slope?
Exercise 22
A 70 kg pilot flies an airplane at 400 km/h (55.6 m/s) in a turn of radius 2 km ( m).
(a) At what angle to the horizontal are the wings?
(b) What is the normal force exerted on the pilot (we often refer to it as pilot's apparent weight)?

Exercise 23
A 60-kg woman is on a Ferris wheel that takes her in a vertical circle of radius 20 m at constant speed.
(a) At what speed would she feel weightless (the normal force is equal to zero) at the top?
(b) At this speed, what would be the normal force exerted on her (her apparent weight) at the bottom?
Exercise 24
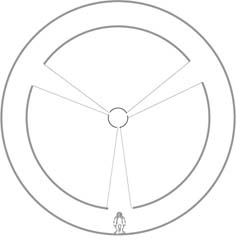
A doughnut-shaped spacestation travels in outer space where the gravitational force is negligible. In order to generate "a feel of weight", the spacestation is rotating with constant speed v. It has a diameter of 2 km (radius m). An astronaut walking in the spacestation is shown in the diagram below. What should be the period of rotation for the astronaut to experience an apparent weight of 20% that on Earth?
Exercise 25
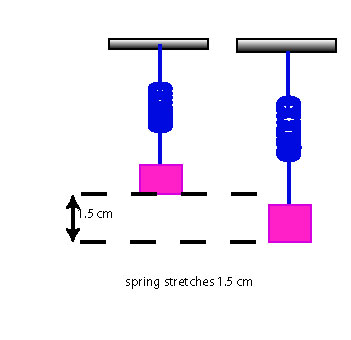
A spring stretches 1.5 cm when it supports a 200 g mass. How much does it stretch when it supports a 250 g mass?
Exercise 26
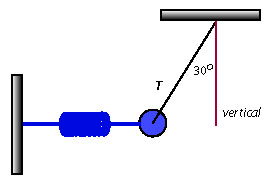
A pendulum bob is held in place by a spring as shown. If the spring constant N/m, and the spring stretches 2 cm, what is the mass of the bob?
Exercise 27
A spring of spring constant N/m supports a mass of 2 kg.
(a) How much does the spring stretch when the spring moves up at constant velocity?
(b) How much does the spring stretch when the spring moves up with an acceleration of ?
(c) What is the acceleration if the spring stretches 0.8 cm?
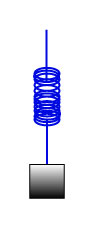
Exercise 28
A 40 kg child is riding in a hot air balloon which is descending with an acceleration of . What is the apparent weight of the child?
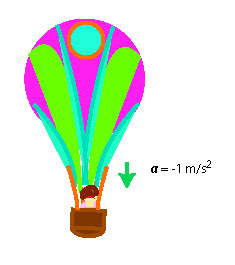
Exercise 29
It is possible to twirl a bucket containing water in a vertical circle without the water spilling out.
(a) What are the forces acting on the water at the highest point?
(b) Why doesn't the water spill out?
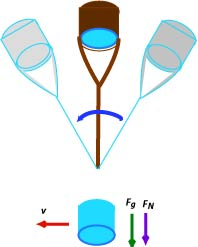
Exercise 30
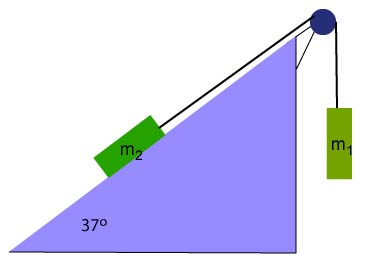
Two blocks, kg and kg are connected as shown in the diagram and move at constant velocity down the incline. Find the coefficient of kinetic friction assuming it is the same for both blocks and the tension in the rope.
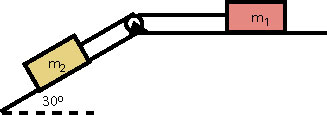
Exercise 31
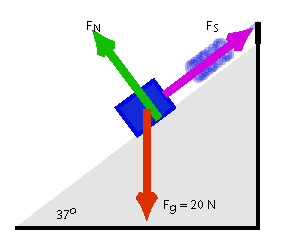
A 5 kg block is on a 37º incline for which = 0.1. It is acted on by a horizontal force of 25 N. What is the acceleration of the block if it is moving up the incline? If its initial speed is 6 m/s up the incline, how far does it travel in 2 s?
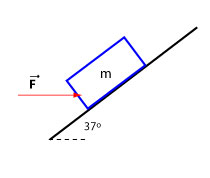
Exercise 32
The minimum stopping distance for a car travelling at an initial speed of 100 km/h is 60 m on level ground. What is the stopping distance when it moves down a 10º incline, or up a 10º incline? Assume the same initial speed and surface.
Exercise 33
A circular off ramp has a radius of 60 m and a posted speed limit of 60 km/h. If the road is horizontal, what is the minimum coefficient of friction required?
Exercise 34
A 5 kg block is subject to a horizontal force of 30 N. It lies on a surface for which = 0.5 and = 0.7. If the block is at rest, what is the frictional force on it? What is the acceleration of the block if it is moving to the left or to the right?
Exercise 35
The moon Io of Jupiter is in a circular orbit of radius km with a period of 1.77 days. The period of another moon, Europa, is 3.55 days. What is the radius of its orbit? What is the mass of Jupiter?
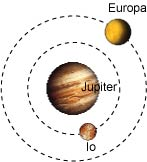
Exercise 36
In November 1984, the space shuttle Discovery was placed in a circular orbit at an altitude of 315 km in order to catch up to the disabled Westar 6 satellite in circular orbit at an altitude of 360 km. Suppose that these two objects were initially on opposite sides of the earth. How many orbits would the satellite have made for the shuttle to be beneath the satellite (that is along a radial line and closer to Earth)? Take = 6370 km.
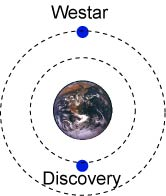
Exercise 37
A particle of mass 4M is at the origin while a particle of mass M is located at x = 1 m. A third particle of mass m is located somewhere in the vicinity of the other two particles. Assume that gravitational forces between particles are the only interactions involved in this problem (in other words, assume that these three particles are located somewhere in outer space.) Where should the particle of mass m be placed so that it is in equilibrium?
Exercise 38
Calculate the strength of the gravitational field at the surface of the following bodies: Neptune ( kg, m), Jupiter ( kg, m), and a neutron star ( kg, km). In all cases, assume that the objects are spheres of uniform density. Assume that the centre of mass is at the centre of the sphere in all cases.
Exercise 39
Estimate the magnitude of the force exerted on the moon by the Earth and by the Sun.
Exercise 40
At what point between the Earth and the Moon does the net force on a spacecraft due to these two bodies vanish? Assume the mass of the Earth is 81 times that of the Moon.
Exercise 41
Use the moon's period of 27.32 days and the radius of its orbit km to find the mass of the Earth. Use the Earth-Sun distance and the period of the Earth to find the mass of the Sun.
Exercise 42
Neutron stars rotate with periods less than one second. The typical radii of neutron stars are just a few kilometers. Let assume that a neutron star rotates with a period of 1 s and has the radius of 20 km. We can estimate the mass of this star from the fact that objects on its surface are bound to remain on it. Determine the mass of this star.
Exercise 43
A 70 kg man is shown enjoying the "rotor" ride at the amusement park. The rotor has a diameter of 4 m and rotates once every 2 s. What is the normal force exerted on the man? What is the force of friction required to keep him from slipping down the wall?
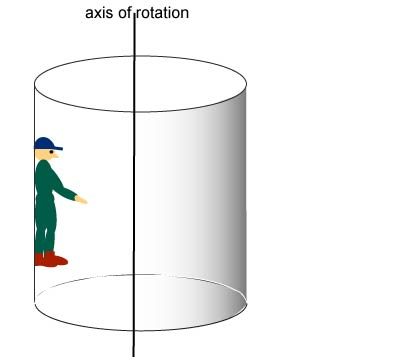
Exercise 44
Two blocks with equal masses kg are connected via a pulley. The coefficient of kinetic friction is = 0.25.
(a) Find the acceleration of the two blocks when is moving down.
(b) Find the acceleration of the two blocks when is moving up.
(c) Determine the mass of so that it moves up at constant speed when kg.