Newtons Laws EX 40

A satellite on its way to the Moon is attracted towards the Earth with a gravitational force of $F_1$. The force gradually decreases as the distance, $x$, between the Earth and satellite increases. At the same time the Moon attracts the satellite with a gravitational force $F_2$ (which increases as the distance to the Moon decreases.) These two forces oppose one other (see the diagram below).

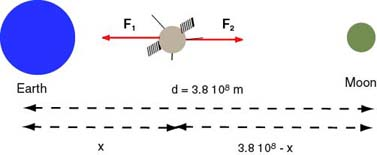
The distance between the Earth and the Moon is $3.810\times 10^8$ m. When the satellite is at a distance $x$ from the Earth then it is at a distance $([3.810\times 10^8]-x)$ from the Moon. We are looking for a distance $x$ at which $F_1+F_2=0$, which happens when the magnitudes of these forces are equal. The gravitational force $F_1$ depends on the mass $m_E$ of the Earth, the mass $m_s$ of the satellite, and the distance $x$ between them; the force $F_2$ depends on the mass $m_M$ of the Moon , the mass $m_s$ of the satellite, and the distance $([3.810\times 10^8]-x)$. We will now write the equation $F_1=F_2$ and replace both $F_1$ and $F_2$ by appropriate formulas in the Newton Law of gravitation.

$\frac{G{m}_E{m}_s}{x^2}=\frac{G{m}_M{m}_s}{([3.810\times 10^8]-x{)}^2}$

Given that the Earth is 81 times more massive than the Moon, we can write: $m_E=81m_M$. Upon substitution into the above, we get:

$\frac{G(81m_M)m_s}{x^2}=\frac{G{m}_M{m}_s}{([3.810\times 10^8]-x{)}^2}$

The constants $G$, $m_M$ and $m_s$ cancel out to leave us with:

$\frac{81}{x^2}=\frac{1}{([3.810\times 10^8]-x{)}^2}$

By taking the positive square root on either side of this equation, we get

$\frac{9}{x}=\frac{1}{(3.810\times 10^8)-x}$

and after cross multiplication and isolation of $x$, we see that $x=3.4\times 10^8$ m.