Newtons Laws EX 41

The Moon moves around the Earth in 27.32 days. Therefore the period of the uniform circular motion of the Moon is $T=27.32days=2.36\times 10^{6}s$. The diagram below illustrates the Moon's orbit around the Earth.

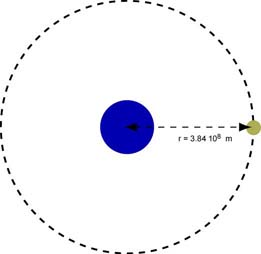
The Moon is in uniform circular motion and therefore it has radial acceleration. To determine its acceleration we first need to determine its speed

$v=\frac{2\pi r}{T}$

and substitute this value into the expression for radial acceleration:

$a_r=\frac{v^2}{r}=\frac{(\frac{2\pi r}{T}{)}^2}{r}=\frac{4{\pi }^{2}r}{T^2}$

The gravitational attraction by Earth is the force that causes this acceleration and thus, we can write Newton's 2nd Law

$\frac{G{M}_E{m}_M}{r^2}=m_M{a}_r=m_M\frac{4{\pi }^{2}r}{T^2}$

By solving for $M_E$ and then by substituting the values for the gravitational constant, the radius of the Moon's orbit and the Moon's period into this equation, we find the mass of Earth to be

$M_E=\frac{4{\pi }^2{r}^3}{G{T}^2}=\frac{4{\pi }^2(3.8\times 10^8{)}^3}{(6.67\times 10^{-11})(2.36\times 10^6{)}^2}=6.01\times 10^{24}kg$