Newtons Laws EX 11

Although these questions appear to be simple, we have to apply the rules we have learned to answer them. We infer from the diagrams that the blocks are stationary and therefore have zero acceleration. Consequently, the net force on each block is zero.

Let's consider (a) - see the diagram below:

Let's assume that the tension is $T_{1}$ in the lower string and $T_{2}$ in the upper string. Then the lower string pulls upward on the block with a force equal to $T_{1}$. Since the block has zero acceleration, then the net force exerted on the block is zero. This means that the force exerted by the string balances the weight of 50 N. Consequently, $T_{1}=50$ N. The lower string pulls on the spring scale downward with a force equal to $T_{1}$ which is 50 N and the upper string pulls on the spring scale with an upward force equal to $T_{2}$. Because the acceleration of the spring scale is also zero we conclude that $T_{2}=50$ N. Consequently, the scale reads 50 N.

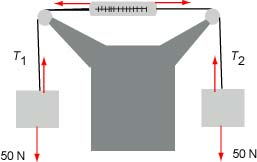
Let's consider (b) - see the diagram below:

Note that since we consider the pulley massless, the tension in the string does not change because of the pulley. Consequently, the tension in the vertical part of the string on the left is the same as the tension in the horizontal part and it is equal to $T_{1}$. Similarly, on the right, the tension is the same in both horizontal and vertical parts and it is equal to $T_{1}$. Since the block on the right has zero acceleration, the tension $T_{1}=50$ N and since the block on the left has zero acceleration, the tension T_2 = 50 N. The tension $T_{1}$ pulls the spring scale to the left and the tension $T_{2}$ pulls the spring scale to the right. Consequently, the spring scale reads 50 N.

Let's consider (c) - see the diagram below:

Using a similar reasoning as in previous examples we will conclude that the tension $T_{1}$ is equal to 50 N. Since the spring scale has zero acceleration, the tension $T_{2}$ must be equal to $T_{1}$ or 50 N. Therefore the scale reads 50 N.