Newtons Laws EX 27

(a) The acceleration of the block is zero so the sum of the forces exerted on the block is zero. There are two forces exerted on the mass, $F_S$ and $F_G$. We choose the x-axis pointing upward. Then we draw the free body diagram

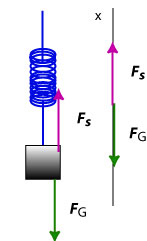
and write the equation since we don't have to compute the components:

$F_S-F_G=0$

It follows from this equation that the magnitude of the force of the spring must be equal to the magnitude of the gravitational force.

$kx=mg$

$x=\frac{mg}{k}=\frac{(2)(10)}{2\times 10^3}=10^{-2}m=1cm$

(b) The acceleration of the block is $2m/s^2$ upwards (the free body diagram is below):

$F_S-F_G=ma$

$F_S=m(g+a)=(2)(10+2)=24N$

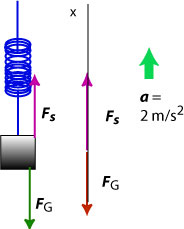
Since the magnitude of the force of spring is equal to

$kx=24N$, we can compute

$x=\frac{kx}{k}=\frac{24}{2\times 10^3}=1.2\times 10^{-2}m=1.2cm$

(c) Here we know the magnitude of the force exerted by the spring $F_S=kx=(2\times 10^3)(0.8\times 10^{-2}=16N$. We will assume that the acceleration points upward and draw the same diagram as in the problem above.

$F_S-F_G=ma$

$16-20=2a$

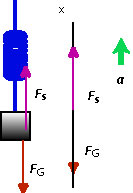
Solving for $a$ we find $a=-2m/s^2$. The negative sign indicates that the mass accelerates downward.