Newtons Laws EX 33

A car is traveling along a circular road of radius 60 m. The diagram below gives the top view of the road and the car, and beside it, the side view of the car sitting on the flat surface of the road. Our system is the car. We don't know its mass but assign it the symbolic value $m$ so that we may go ahead with our calculations.

The side view suggests the following forces acting on the car: $F_{G}$, $F_{N}$, $F_{f}$. The direction of the force of friction can be deduced from Newton's laws. Indeed, circular motion is an accelerated motion, where acceleration points towards the center of the circle. Since the road is flat, acceleration is parallel with the surface of the road. And friction is the only force that acts along the surface, so it is friction that gives the particle (the car) it's acceleration to the right. We conclude that the force itself points to the right. Now we have to think whether we are considering static or kinetic friction. When the car travels along the circle, its wheels don't skid: there is no radial displacement (i.e.: the length of the line connecting the car to the center of the circle is constant.) Consequently, we consider the force as that of static friction.

We orient the axes so that the positive x-axis points toward the right, in the direction of acceleration. Since the car is moving with velocity 60 km/h = 16.7 m/s along a circle of radius 60 m, it has an acceleration of

$a={v^{2} \over r}$

Substituting the given data into this equation, we find that $a={16.7^{2} \over 60}=4.63m/s^{2}.$

The diagram below shows the forces acting on the particle and the associated free body diagram.

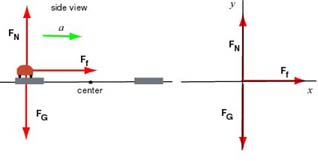
The components of the forces exerted on $m$ are:

Forces	x-component	y-component
$F_{G}$	0	-mg
$F_{N}$	0	$F_{N}$
$F_{f}$	$F_{f}$	0

Note that we will use $g=10m/s^{2}$ in our computations.

First we have to deal with the y-component:

$-mg+F_{N}=0$

This yields $F_{N}=mg$. Substituting for $F_{N}$ into the equation for the force of static friction, we get:

$F_{f_{max}}=\mu _{S}F_{N}=\mu _{S}mg$

Now we proceed to think about the x-component

$F_{f}=ma$

By substituting the force of friction and the acceleration into this equation we find:

$\mu _{S}mg=m(4.63)$

The mass cancels out and solving for $\mu _{S}$ we find $\mu _{S}=0.463$. Now, if the coefficient of static friction were smaller that 0.463, the maximum force of static friction would not be large enough to provide an acceleration of $4.63m/s^{2}$ (so that it cannot be smaller than this value). On the other hand, if this coefficient is larger then 0.463, a force smaller than the maximum possible value will be sufficient to provide the needed acceleration to prevent the skid. Therefore 0.463 is the minimum coefficient of static friction that is required to prevent the car from skidding.