Newtons Laws EX 2

First we focus on the mass $m_2=5$ kg. There are four forces acting on this particle: $F_G$, $F_N$, $F_f$, and $F_T$ pointing towards the string pulling the block. The particle moves down the incline and therefore the force of friction points up the incline. Similarly, we list forces on the mass $m_1=10$ kg. The force of tension pulls the block towards the left.

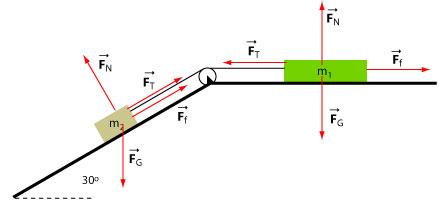
The blocks move at constant velocity and therefore their acceleration is zero. We select the x-axis parallel to the incline and parallel to the horizontal surface as shown in the diagram below.

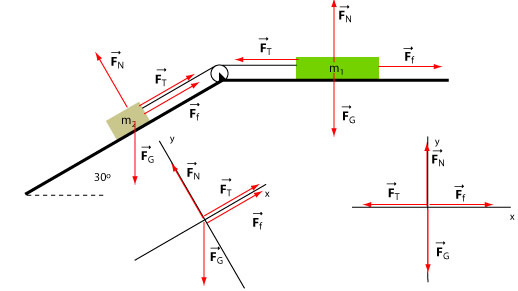
We will deal with each particle separately. First we focus on the mass $m_2=2$ kg. The gravitational force points vertically down and therefore it makes a 30° angle with the negative y-axis; consequently, it makes an angle -120° with the positive x-axis.

The components of the forces exerted on $m_2$ are:

Forces	x-component	y-component
$F_G$	mg cos(-120°) = 50 cos(-120°) = -25 N	50 sin(-120°) = -43 N
$F_N$	0	$F_N$
$F_f$	$F_f$	0
$F_T$	$F_T$	0

Note that we used $g=10m/s^2$ in our computations.

First we have to deal with the y-component:

$-43+F_N=0$

This yields $F_N=43$ N

Now we can proceed to think about the x-component. Using that the acceleration is 0, we can write:

$F_T+F_f-25=0$

We cannot solve this equation immediately, and so, we focus on the mass $m_1=10$ kg.

The components of the forces exerted on $m_1$ are:

Forces	x-component	y-component
$F_G$	0	-100 N
$F_N$	0	$F_N$
$F_f$	15 N	0
$F_T$	$-F_T$	0

First we have to deal with the y-component:

$-100+F_N=0$

This yields $F_N=100$ N.

Now we can proceed to think about the x-component, and because acceleration is 0, we can write:

$-F_T+15=0$

There remains only to solve the following system of two equations:

$F_T+F_f-25=0$

$-F_T+15=0$

Solving for $F_T$, we find $F_T=15$ N and solving for $F_f$ we find $F_f=10$ N.