Newtons Laws EX 9

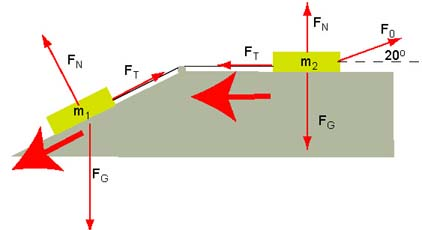
List the forces acting on each block; note that the tension in the rope produces the force of tension at each end of the rope pointing towards the rope.

Now we decide which way the system will accelerate. Since the weight of $m_1$-block is 50 N and the force which pulls the system of the two blocks in the opposite direction is only 10 N, we guess that the system of two blocks will accelerate as the thick arrows show.

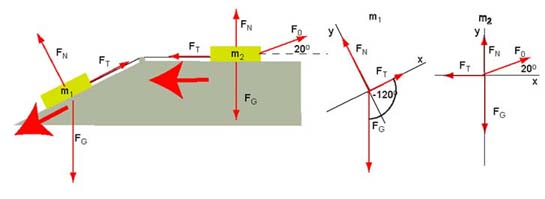
Now we select the system of axis for each of the blocks as a separate system and transfer all the vectors into this system. We determine the angles - we note that the gravitational force makes an angle -120º with positive x-axis in the free body diagram for $m_1$.

	$m_1$		$m_2$
	x-component	y-component	x-component	y-component
$F_G$	50 cos(-120º) = -25 N	50 sin(-120º) = -43 N	30 cos(-90º) = 0	30 sin(-90º) = -30 N
$F_N$	$F_N$ cos(90º) = 0	$F_N$ sin(90º) = $F_N$	$F_N$ cos(90º) = 0	$F_N$ sin(90º) = $F_N$
$F_T$	$F_T$ cos(0º) = $F_T$	$F_T$ sin(0º) = 0	$F_T$ cos(180º) = $-F_T$	$F_T$ sin(180º) = 0
$F_0$			10 cos(20º) = 9.4 N	10 sin(20º) = 3.4 N
Newton's Law	-25 + $F_T$ = 5a (1)	-43 + $F_N$ = 0 (2)	$-F_T$ + 9.4 = 3a (3)	-30 + $F_N$ + 3.4 = 0 (4)

To solve add equations (1) and (3) to find

$-25+F_T-F_T+9.4=5a+3a$

Solving for $a$ we find $a=-1.95m/s^2$. Now substitute for $a$ in the equation (1) we find

$-25+F_T=5(-1.95)$

Solving this equation for $F_T$ we find $F_T=15.25$ N.