Equations of Motion

Helena Dedic

Derivation of Equations of Motion

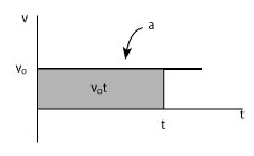
Consider a v-t graph for an object moving with constant velocity.

• Motion with constant velocity implies that the acceleration is equal to zero and therefore the v - t graph is a horizontal line.

$v(t)=v_o$

• The displacement is the area under the v - t graph

We write $\mathrm{\Delta }x(t)=v_{o}t$

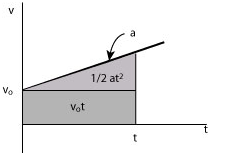
• Motion with constant acceleration implies that the velocity is a linear function of time. Given that the initial velocity is $v_0$ we can write

$v(t)=v_o+at$

where the acceleration is the slope of the graph and$v_o$ is the intercept.

• The displacement is the area under the v - t graph

We write

$\mathrm{\Delta }x(t)=v_{o}t+\frac{1}{2}a{t}^2$
 

• The displacement in both cases is $\mathrm{\Delta }x(t)=x(t)-x_o$

• There are two independent equations describing motion with constant acceleration and five variables: $\mathrm{\Delta }x(t)$, v(t), $v_0$, a and t. Consequently, in any problem we can solve for two of those variables and three other must be given.

• We can derive another useful equation by eliminating t from the two equations above.

We begin with equation

$v(t)=v_o+at$

We isolate t:

$t=\frac{v(t)-v_o}{a}$ 

Then we substitute for t in the equation for the displacement:

$\mathrm{\Delta }x(t)=v_o\left(\frac{v(t)-v_o}{a}\right)+\frac{1}{2}a{\left(\frac{v(t)-v_o}{a}\right)}^2$ 
 

We will now multiply both sides by 2a. This step will eliminate fractions from this equation.

$2a\mathrm{\Delta }x(t)=2a{v}_o\left(\frac{v(t)-v_o}{a}\right)+2a\frac{1}{2}a{\left(\frac{v(t)-v_o}{a}\right)}^2$ 
 

This leads to:

$2a\mathrm{\Delta }x(t)=2v_o(v(t)-v_o)+(v(t)-v_o{)}^2$ 
  

Expanding:

$2a\mathrm{\Delta }x(t)=2v_{o}v(t)-2v_o^2+v^2(t)+v_o^2-2v_{o}v(t)$ 
  

which leads to:

$2a\mathrm{\Delta }x(t)=-v_o^2+v^2(t)$ 
  

This can finally be written in the form:

$v^2(t)=v_o^2+2a\mathrm{\Delta }x(t)$ 

Exercises

• Problem solving using equations of motion

Free Fall

• Free Fall

Projectile Motion

• Projectile Motion