Series Circuits

  Series Circuits 

What happens when current flows in a circuit?
Up until now, we have examined the flow of electric current through wires and resistors in somewhat artificial situations. That is, they’re “artificial” because the charges have been flowing in one end of the resistors and then out the other end, without our knowing where the charges came from, and also without knowing to where they’re going. We have said that the charges lose energy as they flow through the resistors, but we have not said what is providing energy to the charges. (If nothing was providing energy to them, the charges in the current would soon lose all their energy and could no longer flow through the resistors.) We have concluded that there must be an electric field present (and so a V) to provide a force that “pushes” the charges through the resistor. However, we haven’t said what provides the source charges to create that electric field.

We have assumed that the flow of current is “steady” and continuous – without a pile-up of charge in any one location. One arrangement that could achieve this is to have the charges flow continuously in a closed path (for instance, in a circular route). Such a continuous closed path for the flow of current is called an electric circuit. A device that is very often used to provide energy to charges flowing in a current is the battery (Chapter 4 Notes, page 3). The battery also provides the source charges that create the electric field in the wires. So we can now illustrate a very simple circuit, including a resistor connected to a battery with “perfectly conducting” wires, with a diagram such as this:

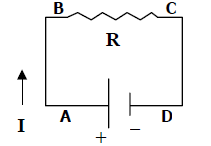
(We have indicated four different points in this circuit – A, B, C and D – for the discussion to follow, and we have also showed the direction of flow of current I.) In order to discuss this circuit, we must recall our definition of “perfectly conducting” wires. We assume that all wires (indicated in the circuit diagram by straight line segments) are “perfect conductors” which do not hinder the flow of electric charge at all. Therefore, we assume that these wires
(a) have no resistance (R = 0), and that therefore
(b) there is no change in potential V at different positions along a wire ($\Delta V$ = 0 between any two points on the wire). In reality, metal wires do have some resistance, but it is quite small compared to the resistance of other circuit components. Therefore it is a very good approximation to neglect it, and to assume that R for a wire is zero.
In this circuit, there is only one path for the charges to follow; each charge in the current flow must follow the same route. (Here, the charges flow out of the positive terminal of the battery, in to the left side of the resistor, out of the right side of the resistor, and then back in to the negative terminal of the battery.) A circuit with only one current path is called a series circuit. Now let’s consider some questions about charges flowing in a current through this circuit.
Question #1: A charge is moving around the circuit as part of current I. At point A, this charge has PE equal to x joules. When it returns to point A, having completed one circuit, is the PE of this charge greater than, less than, or equal to x joules?
Answer: Equal to. Remember that the potential energy of a charge has a specific value for each different location. Whatever path that charge may take in traveling away from its initial position, when it returns to that position it must have exactly the same potential energy with which it started. (Here we are assuming that the source charges creating the electric field are not varying or moving; this will be the case if we have “steady” [unchanging] currents.)
Let’s consider what happens to the potential energy of that charge as it moves from point to point in the circuit.
Question #2: Will the PE of the charge increase, decrease, or remain the same as it moves (a) from A to B; (b) from B to C; (c) from C to D.
Answers: (a) remains the same; (b) decreases; (c) remains the same. To understand these answers, we might first substitute V for PE and consider the same questions. As a charge moves along a wire segment – for instance, from A to B, or from C to D – its potential V does not change (since the “perfectly conducting” wire segment is all at the same potential). Since PE = q$\Delta V$

and $\Delta V$ 
= 0, we see that the potential energy of the charge does not vary as it moves through the wire.

However, as discussed in Chapter 5, the charge experiences a potential decrease as it flows through the resistor. Therefore, on the path from point B to point C, the charge’s potential energy must also be decreasing. As we discussed in Chapter 5, the average kinetic energy of the charges flowing in the current is essentially constant. (The contribution to the kinetic energy made by their flow through the wire is also very small, since the average velocity of the charges in the direction of the current is only about 10–4 m/s!). So the total energy of the charges is decreasing. As the charges in the current flow through the resistor, they make many collisions with the atoms in the resistor. This makes these atoms vibrate, and in this way causes the resistor to get hot (and perhaps even give off light, if the resistor is actually the filament of a light bulb). So there is a transfer of energy from the charges in the current to the material in the resistor.

In view of all of this, let us now ask:
Question #3: As the charges flow from point D to point A, does their potential energy increase, decrease, or remain the same?
Answer: Increase. In Question #1, we decided that the PE of the charges must return to the original value that it started out with at point A. Since the PE decreased as it went through the resistor, it must now increase as it goes through the battery. This makes sense, since we have already concluded that the battery must be supplying the energy to the charges that they are losing as they go through the resistor. Now, we can answer Question #4: Is the value of V at point A higher, lower, or the same as the value of V at point D? Answer: Higher. The positive charge gains potential energy as it goes from D to A, so it must be experiencing an increase in potential V as well since $\Delta V=\Delta PE/q$ . If $\Delta PE>0$ and q > 0, then $\Delta V$ must also be greater than zero. (Note that for a negative charge q < 0, and so an increase in PE implies a decrease in V.)

As we discussed in a previous wiki, an ideal battery always maintains a constant, unchanging value of V between its terminals. The battery uses chemical means to physically separate positive and negative charges, “pushing” them against the attractive forces that normally would bring them together. The result is that a battery creates a potential difference – a $\Delta V$ 

– within itself (and an electric field as well). In a sense, it “drags” a positive charge away from the negative terminal, pushes it toward the positive terminal, and then on through the wires away from the positive terminal. The forces involved in this “pushing” are chemical bonding forces.
Finally, we may put all of these pieces together to find some general rule governing this type of circuit.
Question #4: As a charge moves around a circuit in a complete loop, is the sum total of the increases in V that it experiences along the way greater than, less than, or equal to the sum total of the decreases in V that it experiences?
Answer: Equal to. We know that the increases in PE must balance out the decreases in PE (since it returns to its original value of PE); therefore, the same must be true for the increases and decreases in V.
We can now summarize the main points brought out previously that relate to the simple series circuit:
1. An ideal battery maintains a constant potential difference V between its terminals. This potential difference V is usually called the “battery voltage,” and satisfies the relation $\Delta V=V_{+}-V_{-}$

V = V+ – V– , where V+ is the potential at the “positive” terminal, and  V–  is the potential at the “negative” terminal. By definition, the positive terminal is the one at the higher potential. (The positive terminal has an “excess” of positive charges, and creates a net electric field that pushes positive charges away from that terminal and on through the wire.)

2. As positive charges flow through a battery from the negative terminal to the positive terminal, their potential energy increases. There is a transfer of energy from the battery to the flowing current.
3. As positive charges flow through a resistor, their potential energy decreases, and so they flow from the side of the resistor at the higher potential to the side of the resistor at lower potential. The kinetic energy of the charges is essentially unchanged, and so their total energy decreases. There is a transfer of energy from the charges in the current to the material comprising the resistor.
4. Wires are made of conducting materials that offer very little resistance to the flow of current. We will always assume that wires are perfect conductors such that Rwire = 0, and so V = 0 between any two points on the wire.
5. The algebraic sum of the potential changes (increases minus decreases) experienced by charges as they go once around a full circuit is equal to zero. (The magnitude of [the sum of the increases] is equal to the magnitude of [the sum of the decreases].)