Magnetic Induction

Kreshnik Angoni and Kevin Lenton
Worksheet.docx
Worksheet.pdf

Additional Problems
Additional Problems2


Other Resources:

• Haliday & Resnick, Fundamentals of Physics 30.1-5
• Openstax
• Printable version

Learning Objectives

After reading this page, watching the videos and reviewing the exercises, you will be able to:

• Understand the conditions required for magnetic induction.
• Know the equations to calculated induced potential, and how to apply them.
• Know to avoid some common misconceptions.
• Apply the concepts to some induction problems.

Some Experimental Observations

Just as currents produce magnetic fields, changing magnetic fields can produce currents in conductors.
Look at these videos to see some of the amazing effects of magnetic induction.

Beginning to Build a Model of Magnetic Induction

A conductor rod that slides at constant speed on two conducting rails terminating in a galvanometer is part of a closed passive circuit (without a potential difference); generally, there is no current in the circuit. But, if the rod moves inside a magnetic field, the galvanometer G shows a current passing through the circuit (fig.1)

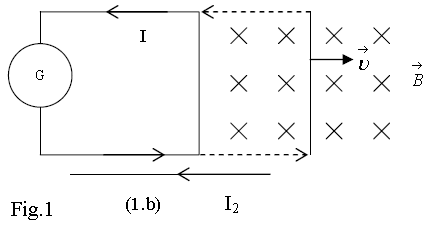
So, “a current appears in a conductor moving inside a magnetic field ”. Actually, this is quite expected from the effects of magnetic force. The free electrons inside the conductor move with velocity v with respect to the magnetic field B .
The magnetic force ${\vec {F_{B}}}=-e{\vec {v}}\times {\vec {B}}$ (1)
sets the electrons in movement “down” and a current (in the opposite direction) passes through the circuit as long as the wire moves.

Consider now the rod at rest and a current $I_{2}$ passing through a second wire located close by as shown in figure 1. We know that this current must have a magnetic field around it. This field will also be in the area marked out by the circuit. Observations show that, starting from the moment t=0 (when the current starts in the second wire) and during a very short time interval ( $\Delta t$ ) the galvanometer needle moves; so “a current appears in the circuit”. Also, for longer times (steady state) t > t+$\Delta t$, the current in the circuit returns to zero. This was a new effect observed for the first time by Joseph Henry.
It is clear that, in the two cases, the appearance of an electric current in a circuit is due to “some kind of action from the magnetic field”. Before going into a better understanding of these phenomena, keep in mind that the current means charges in movement and this requires the presence of an electric field.
So, this action of the magnetic field is consistent with the creation of an electric field inside the circuit wires. Electromagnetic induction is the induction of a current inside a circuit due to a magnetic field.

Definition of Magnetic Flux

From an electrical point of view, the fact that a current passes through the circuit means that an emf (${\mathcal {E}}$ ElectroMotiveForce=Voltage=potential difference) is operating on the circuit. Let’s define the magnitude and the direction of this emf.
Consistent observations show that the magnitude of this induced emf is related to the change of magnetic flux $\Phi _{B}$ inside the closed circuit. The flux $\Phi _{B}$ of a magnetic field B through a loop,(or a closed circuit) is defined as
$\Phi _{B}={\vec {B}}\cdot {\vec {n}}A={\vec {B}}\cdot {\vec {A}}=BAcos\theta$ (2)

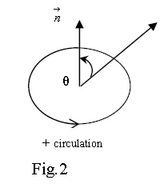
${\vec {A}}=A{\hat {n}}$ is the area vector of the loop. A is the magnitude of the area of loop and ${\hat {n}}$ is the unit vector of the loop direction, defined as being perpendicular to the loop surface. Then, after aligning the thumb with the ${\hat {n}}$ direction, the right hand rule gives the positive sense of the circulation ${\vec {B}}$ in the loop along the direction of your curled fingers (=right hand curl rule).
Basically Flux is a measure of the magnetic field going through a certain area.

Different Ways of Changing the Flux

Note that for a given field strength ${\vec {B}}$ , the flux $\Phi _{B}$ can be changed by changing the loop area (fig 3a; the loop goes from a circle to an elipse) or by changing the angle (fig3.b). The rotation of the loop (changing the angle) is the situation generally met in practice (AC generators, electric motors,).

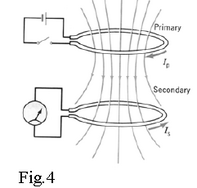
Also, you can change the flux $\Phi _{B}$ by changing the magnitude of the ${\vec {B}}$vector. In fig.4, the magnetic field produced by the primary circuit passes through the secondary circuit. You can change the magnitude of the ${\vec {B}}$ field inside the area of the secondary circuit by changing the current $I_{primary}$ in the primary circuit.

Units of Magnetic Flux

The unit of magnetic flux in the SI system is the Weber (Wb). From expression (2), you can find that
$1Wb=1T\cdot 1m^{2}$ (3)

In our introduction for flux, we were referring to a loop inside a

uniform magnetic field. In a more general situation, the magnetic field may change from one location to another inside the loop and the flux is defined as the sum of all local contributions. This means that the general formula for the magnetic flux through a real loop must be calculated as
$\Phi _{B}=\underbrace {\oint \oint } _{\textrm {CircuitSurface}}{\vec {B}}d{\vec {A}}$ (4)
That is to the say the integral of all the contributions to flux across the area in question. Most problems however will have a uniform B field inside the loop.

Faraday’s Law: The Induced EMF is equal to the Rate of Change of Magnetic Flux

Faraday introduced the mathematical definition for the induced emf. He found that the magnitude of induced emf is equal to the rate of change of the magnetic flux through the loop:
$|{\mathcal {E}}|=|{\frac {d\Phi _{B}}{dt}}$| (5)
Applying the chain rule:

$|{\frac {d\Phi _{B}}{dt}}|={\frac {d(BAcos\theta )}{dt}}={\frac {d(B)}{dt}}Acos\theta +B{\frac {dA}{dt}}cos\theta -BAsin\theta {\frac {d\theta }{dt}}$(6)
Faraday’s Law shows that there are three ways to induce an emf ( change B, change A, or change angle ).
Important: In practice, usually you deal mainly with achange of the B field or the angle.

Lenz’s Law: The Induced EMF always Opposes Changes to Flux

The direction of the induced emf is defined by Lenz's law. Lenz's law is a particular expression of action-reaction behaviour .
It says that: While the exterior action is changing the flux, the induced emf in a circuit has a direction such that the related current produces a magnetic field which tends to keep the previous value of magnetic flux into the circuit.

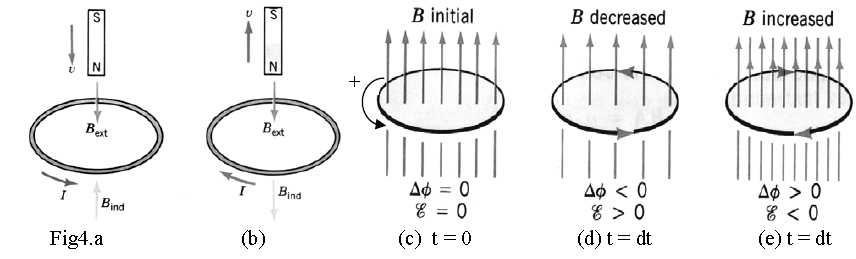
In fig4a the external action is increasing the flux; the induced current has a direction such that the related field $B_{ind}$ (directed upside) works against the exterior action (by decreasing the net field). In fig4.b the external action is decreasing the flux; the induced current has a direction such that the related field $B_{ind}$ (directed downside) works against the exterior action (by increasing the net field).
In fig4.c the system is in a stationary state; there is no flux change through the circuit (e = 0). In fig4.d the external field magnitude is decreasing ($\Phi _{B}$ < 0) and the induced current direction is tending to compensate for external action by creating an “up” directed Bind. In fig4.e the external field is increasing ($\Phi _{B}$ > 0) and the induced current direction is tenting to compensate for external action, by creating a “down” directed induced magnetic field $B_{ind}$ which tends to decrease the net magnetic flux.
Now, let’s use the figures 4.c,d,e to include Lenz’s law into expression (5). At t = 0, there is a field ${\vec {B}}$ through the circuit area. We chose the area vector A directed parallel to ${\vec {B}}$ so that at t = 0 FB is positive. This way we fix the selection for the positive direction (fig4.c) of the current and emf around the circuit. Then, at a moment t = dt, the figures 4.d,e show that the sign of induced emf is the opposite of sign at flux change .FB. So, the Faraday-Lenz law has the form

${\mathcal {E}}=-{\frac {d\Phi _{B}}{dt}}$ (7)
In the case of a coil with N loops Expression (7) becomes ${\mathcal {E}}=-N{\frac {d\Phi _{B}}{dt}}$ (8)

Additional Points

a) Where is the source of the induced emf located? In the case of electromagnetic induction, the emf source is the magnetic field itself. It is distributed along the whole of the circuit and its action is distributed around the whole circuit.
b) Lines of a field are used to visualize the field direction and its magnitude (their density at a given location is proportional to the magnitude of the B field at this point) but they do not have any physical meaning. That is to say they are merely a tool to help describe the physics.

Whereas the magnetic flux is a basic physical quantity at the origin of a natural phenomenon.

c) The change of magnetic field B induces an electric field E which produces a current into the circuit.
This current induces an additional magnetic field in the surrounding space which brings a change of magnetic flux and so on…. This short comment shows that there is a close relationship between the changes of magnetic and electric fields. In fact, electromagnetic induction has implications far beyond: It is at the origin of all types of electromagnetic waves (light, TV, radio, X-rays,etc.).

GENERATORS OF ELECTRIC CURRENT

Essentially, an electric generator is a coil with N turns that rotates at (constant) angular velocity.
($\omega$ ; $\theta =\omega t$) inside a uniform magnetic field (Fig.5) and its function is based on electromagnetic induction. Assume that at t = 0 the plane of the coil is perpendicular to ${\vec {B}}$ and also that the Area vector ${\vec {A}}$ parallel ($\theta =0$) to ${\vec {B}}$ . Then, at t = 0 the flux through the coil $\Phi _{B}=N({\vec {B}}\cdot {\vec {A}})=NBAcos\theta =NBA$
is positive and maximum.

If the coil starts to rotate as shown, the angle between th two vectors ${\vec {A}}$ and ${\vec {B}}$ increases, the magnetic flux changes. At a moment $t\neq 0$ the angle between the vectors is $\theta =\omega \times t$ and the flux is decreased to
$\Phi (t)_{B}=N{\vec {B}}\cdot {\vec {A}}=NBAcos\omega t$ (9)
The equation (8) shows that if the coil is induced the emf is
${\mathcal {E}}=-N{\frac {d\{\Phi _{B}}{dt}}=NBA\omega sin\omega t$ (10)

This positive emf produces a current which flows in the positive direction of the circulation in the coil as shown in the figure.
From expression (10) you can see that the induced emf is maximum ${\mathcal {E}}_{0}=NAB\omega$ (11)
when $\theta =90$ i.e. when ${\vec {A}}$ perpendicular to ${\vec {B}}$ which means the coil plane is parallel to the ${\vec {B}}$ field.
Now we can rewrite the expression (10) in the form
${\mathcal {E}}={\mathcal {E}}_{0}sin\omega t$ (12)

This expression shows that the induced emf and consequently the current in the coil change their direction sinusoidally. So, an alternating sinusoidal emf (fig.6) (and current) is induced in the coil. In a real AC generator the current goes out of coil into the external circuit by the use of a set of two brush contacts that slide on two rings which rotate together with the coil : the commutators(fig.7).

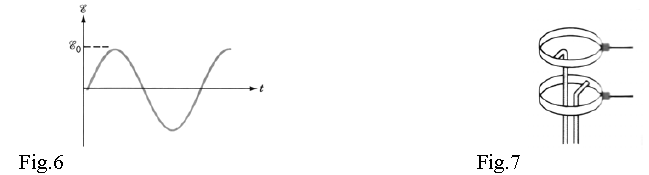
The commutator is a set of two half-rings welded to coil wires (from inside, Fig.8) and sliding over two fixed brushes (from outside). The commutator rotates with the coil. Let’s consider the moment when $\theta =90^{\circ }$ (i.e. when ${\mathcal {E}}=+{\mathcal {E}}_{0}$) and the current is sent outside by the left side brush, as presented in fig.8.

When the coil is rotated by $90^{\circ }$ (i.e. $\theta$ becomes $180^{\circ }$) the direction of the current in the coil is inverted but at that moment the “ex-right side half ring” contacts the “ex-left side brush”. So, the brush on the left always receives current in the same positive direction and sends it on to the external circuit. This device transforms an alternating current into a direct current pulse (Fig.9).
Wheatstone improved the quality of DC current (by smoothing the pulses see Fig.10) by using a system of multiple coils and commutators oriented at different angles. This improvement gives us the DC generators we use today.

MOTIONAL EMF: Induction by changing the Area

Let’s consider a conducting rod with length l moving at constant velocity perpendicular to a uniform magnetic field (Fig.11). Due to magnetic force ( ${\vec {F_{B}}}=-e{\vec {v}}\times {\vec {B}}$) the free electrons move to the lower end and leave a net positive charge at the upper end of rod. This situation builds up an electrostatic field $E_{0}$ directed downward. The related electrostatic force acting upon the electron ${\vec {F_{E}}}=-e{\vec {E_{0}}}$
is directed in opposite sense of ${\vec {F_{B}}}({\vec {F_{E}}}\uparrow \downarrow {\vec {F_{B}}}$
The magnitude of electric force ${\vec {F_{E}}}$ F increases with the increase of charge concentration at rod’s ends.

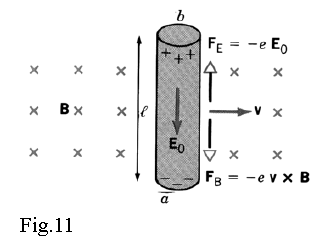
After a short interval of time it becomes equal to magnitude of ${\vec {F_{B}}}$ and the electrons stop moving any more versus the rod’s ends because the exerted net force becomes zero. In this way a steady state equilibrium is set up. Starting from this moment $BE_{0}=evB\ \ \ i.e.\ \ E_{0}=vB$ (13)
At steady state equilibrium there is a potential difference between rod’s ends $V_{b}-V_{a}=E_{0}l=Bvl$ (14)
If referring to terminology used for electric circuits, one might have to say that the charge separation and the potential difference are built by the presence of an emf inside the rod. This kind of emf is known as motional emf. Since no current is flowing through the rod one finds easily that ${\mathcal {E}}=V_{b}-V_{a}=Bvl$ (15)

What is the source of motional emf? To answer this question one must look closer at the work done moving the electrons. There are two forces that act on the rod; a) the magnetic field and b) the external force that moves the rod right side. We will consider the action of each of them separately.
a) The Magnetic Field Force
Each electron has two velocity components; ${\vec {v}}$ along the rod motion and ${\vec {v_{D}}}$ (drift velocity) directed downward (fig.12). The magnetic field interacts with both velocities.

The magnetic force on the electrons from the velocity of the rod is
${\vec {F_{1_{B}}}}=-e{\vec {v}}\times {\vec {B}}$
This force gives a power “the work per 1sec” of ($P={\vec {F}}\times {\vec {v_{net}}}={\vec {F}}\times ({\vec {v}}+{\vec {v_{D}}})$ ) $P_{1}={\vec {F_{1_{B}}}}\cdot ({\vec {v}}+{\vec {v_{D}}})=(-e{\vec {v}}\times {\vec {B}})\cdot ({\vec {v}}+{\vec {v_{D}}})$ (16)
The magnetic force on edue to its drift motion is
${\vec {F_{2_{B}}}}=-e{\vec {v}}\times {\vec {B}}$ and it would Provide a power equal to
$P_{2}={\vec {F_{2_{B}}}}\cdot ({\vec {v}}+{\vec {v_{D}}})={\vec {F_{2_{B}}}}\times {\vec {v}}=-(-ev_{D}B)v=(evB)v_{D}$ (17)

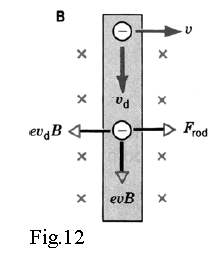
So, the net power provided by magnetic field on each electron is $P=P_{1}+P_{2}=-(evB)v_{D}+(evB)v_{D}=0$ (18)

This result does make sense because the magnetic forces are perpendicular to the velocity and therefore perpendicular to the displacement at any moment.
Hence, at any moment, their dot product is zero; so a magnetic force can never do work.

b) The Force from the Moving Rod.
This force ${\vec {F_{RodonElectron}}}$ is exerted by the rod on the electrons and it has the same direction as ${\vec {v}}$.
From Fig.12, you can see that the net force acting on each electron in the direction of the rod movement has two components ${\vec {F_{Total_{electron}}}}={\vec {F_{RodonElectron}}}+(-e{\vec {v_{D}}}\times {\vec {B}})$ (19)
Since the electron is moving at constant velocity right side (as a particle of the rod) it comes out that the net force exerted on it is equal to zero. So, one gets:
$F_{RodonElectron}-ev_{D}B=0\longrightarrow F_{RodonElectron}=ev_{D}B$ (20)

If the conductor has “n” (electron density) free electrons for m3, a section “A” and a length “l”, it contains in total “n*A*l” free electrons. Since the same “part of rod force” is applied on each of them it comes out that the net force applied on all free electrons in the rod has the magnitude
$F_{rod}=nAl\cdot F_{RodonElectron}=nAl(ev_{D}B)=(nAev_{D})lB=IlB$ (21)

This result is not “unpredictable” if we remember that this is the magnitude of force exerted by magnetic field “B” on the wire with length “l” carrying the current “I”. The external force must balance the magnetic force action so that the “wire can move at constant velocity”.

From the energetic point of view you can conclude that, the work done by the external force goes into moving the rod (motion at constant velocity) and to producing the motional emf (15).
Note that, although the magnetic force does no work by itself, it acts as a kind of intermediary agent that converts a part of the external mechanical work into electrical energy.

Examples

1. A magnet is poked North Pole first into a solenoid. Determine the direction in which the induced current flows and whether the magnet and solenoid attract each other or repel each other.

2. A Square coil is made up of 10 turns and has a side equal to 10cm. The coil is flattened by pulling on the sides in 0.2 s. The coil's resistance is 10 $\Omega$. What is the magnitude and direction of the induced current?

3. A circular 20 turn coil has a diameter of 7.5 cm. It lies in a uniform 0.1 T magnetic field that points out of the page. It is rotated a 1/4 turn, from perpendicular to parallel to the field.
a)How quickly must this be done such that the induced voltage is 1.5V and in what direction will the current flow?
b)You have a power supply that can deliver 5A. How would you produce the magnetic field used in this problem?

4. A 1.5m bar is pulled to the right at a steady 5m/s perpendicular to a uniform 0.75 T magnetic field directed out of the page. The parallel metal rails are connect to a 25 $\Omega$ resistor. You may ignore the resistance of the bar and rails.
a) What is the force vector required to keep the bar moving at 5m/s?
b) At what rate is energy dissipated in the resistor?
c) On the picture indicate the positive and negative ends of the metal bar, and the direction that current moved in the resistor?
d) What is the current in the resistor if the magnetic field is now at an angle of 70 degrees to the vertical? (the bar is still moving at 5m/s)