Motion of a Charged Particle in a Magnetic Field

Kreshnik Angoni and Kevin Lenton
Worksheet.docx
Worksheet.pdf

Additional Problems


Other Resources:

• Haliday & Resnick, Fundamentals of Physics 28.4,6-7
• Openstax
• Printable version

This situation happens frequently in nature(ex: deflection of high-energy charged particles around earth) and is widely used in technology (ex: Confinement of particles in a plasma gas, deflection and focusing of charged particles in an accelerator or electrons in an old fashioned TV CTR tube.)

MOTION IN A UNIFORM MAGNETIC FIELD (mainly met in technological applications)

We will consider the case when the velocity of the particle is perpendicular to B separately to when the velocity is not perpendicular to B .

A. Particle velocity perpendicular to B (Fig.1).

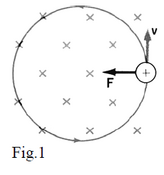
Let’s take, for simplicity, the case when q is positive.

The magnetic force exerted on the charge has a direction perpendicular to both ${\vec {v}}$ and ${\vec {B}}$.
Remember that when any force is perpendicular to the direction of motion ${\vec {v}}$ you always get some sort of circular motion: centripetal force provides a centripetal acceleration: direction towards the centre of the circle. This is exactly the situation here. That is to say, whenever a charged particle enters a magnetic field it performs some sort of circular motion. Let’s assume that the magnetic force is the only acting force on the particle (neglecting gravity).
This force is perpendicular to the particle movement and it will play the role of a centripetal force. Its magnitude is
$|F_{B}|=qvB$(1)

We know that this particle will move in a circle
and from the second law of Newton we can write:
$\sum F_{radial}=ma_{radial}$
$F_{B}=m{\frac {v^{2}}{r}}$
$qvB=m{\frac {v^{2}}{r}}$
$qB=m{\frac {v}{r}}$

From the equation (2), one finds the circle radius as $r={\frac {mv}{qB}}$
If the circumference of the circle is $C=2\pi r$ and the particle makes a full revolution in one period T then:

$v={\frac {distance\ for\ 1rev}{time\ for\ 1rev}}={\frac {2\pi r}{T}}$
$T={\frac {2\pi r}{v}}={\frac {2\pi m}{qB}}$
The frequency is the inverse of the period. Therefore:
$f_{C}=1/T={\frac {qB}{2\pi m}}$

Note that in this type of situation:

a) The particle speed is not affected by the magnetic field.(only its direction changes, not its magnitude)
b) The rotation period and frequency does not depend on the particle speed.
c) Particles with the same ratio (q/m) rotate with equal frequency fC.

Application: the Cyclotron

This type of movement is characteristic of a special type of charge particle accelerator called cyclotrons and the frequency of one revolution fC is known as cyclotron frequency. In this situation the magnetic field does not perform work and the energy of the charged particle is not affected by the magnetic field. Meanwhile, the main duty of an accelerator is the increase of particles’ energy. In cyclotron devices one uses the electric field to increase the particle energy.

  A Cyclotron device is constituted by two half cylindrical parts separated by a small gap. A uniform magnetic field is directed perpendicular to the surface of cylinders and an alternating potential difference is applied between the two parts of cyclotron. The charged particles are produced by an ion source at the centre of this system. The electric field in the space between the two parts at centre accelerates the charged particle first and gives them an initial velocity perpendicular to the magnetic field. Once inside the cyclotron cylinder, there is no more electric force. Rather the magnetic force makes the particle bend around. Once the particle finishes the half circle, the potential switches sign and accelerates the particle across the gap between two cylinders in the other direction.

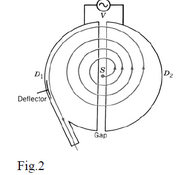
Fig.2

So, each time the particle passes through the gap its kinetic energy increases by

$\Delta KE=qV$ (6)

and the radius of the circle increases (because the particle is now moving faster). When the particle reaches the desired energy it is moving around the outside edge of the cyclotron and it can shot out of the cyclotron, and used, for example to bombard a target.

The fact that the particle rotates at all times with a constant frequency is a big advantage for cyclotrons. You just have to calculate fC for a given type (q/m value) and apply an alternating voltage with a frequency equal to 2*fC . A modern cyclotron has a radius ~ 2m and is used mainly to accelerate protons instead of electrons. This is because electrons have such little mass their velocity quickly approaches the speed of light and special relativity applies. Particularly, the mass increases. The immediate consequence is a change in period of rotation that requires a continuous modification of frequency for alternating the potential. We have the technology: The synchrotron is a more complicated device that adjusts the frequency of alternating potential for relativistic particles.

B: Particle velocity not perpendicular to B

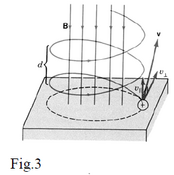
We consider again only positive charge. For any motion, you can break the velocity vector into components: perpendicular to B ${\vec {v_{\perp }}}$ and parallel to B ${\vec {v_{||}}}$. The magnetic Force perpendicular to B ( $F_{B}=qv_{\perp }B$ ) produces circular movement with period $T={\frac {2\pi m}{qB}}$, as seen above.
The parallel component velocity produces no magnetic force: the particle simply moves parallel to the field lines with this constant velocity (see Figure 3). During one period T Fig.3 the particle moves along this direction by:
$d=v_{||}T=v_{||}{\frac {2\pi m}{Bq}}$ (7)
So, the net movement of the particle follows a helical path, orientated with the magnetic field.

Non-UNIFORM MAGNETIC FIELD (particles in a plasma gas)

A plasma gas is a medium with very high temperature and any material used for its confinement would be melted. So, one uses this type of magnetic fields to keep particles inside a restricted space. These fields are known as “magnetic bottles”. As the radius of circular motion is $R\propto 1/B$ , it turns out that, R decreases in any region of space where B increases (observe close to the coils in fig.4). Also, due to the B-field orientation (at any point the direction is always tangent to the field line at that point) the magnetic force is directed towards the region of weaker field no matter what the position of the particle (“seeking the bottle center” at fig. 4). This means that there exists a force component directed in the opposite direction to the velocity. This component slows down the motion of particle along field direction and, if the magnitude of the velocity is not too large, it reverses the direction of motion; the particle returns back to the “center of magnetic bottle”. In this way, once the particle is inserted in a magnetic bottle it remains trapped there inside.

Our sun is a good example of a plasma, and plasma cork-screwing along magnetic field lines is known as a solar flare. The Northern Lights are caused by charged particles (from the sun) corkscrewing along the magnetic field of the earth and hitting the atmosphere at the North (and South) Poles.

CHARGED PARTICLE MOVING IN A MAGNETIC FIELD AND AN ELECTRIC FIELD SIMULTANEOUSLY

When a charged particle enters a space region where an electric field E and a magnetic field B superimpose, two forces are exerted on the particle;
the electric force ${\vec {F}}_{el}=q{\vec {E}}$ and
the magnetic ${\vec {F}}_{B}=q{\vec {v}}\times {\vec {B}}$ .
So, the net force (known as Lorentz force) acting on the particle is
${\vec {F}}_{net}=q({\vec {E}}+{\vec {v}}\times {\vec {B}})$(8)

In general, it is difficult to predict the path followed by a charged particle under the effect of Lorentz force. The simplest cases concern two fields either parallel or perpendicular to each other. We will consider the case of two fields perpendicular to each other. Let’s select a reference system where the electric field is directed along the y axis; the magnetic field is directed along the z axis and the charged particle +q enters this region at the origin with velocity v directed along the x axis (see Fig. 5). So; ${\vec {E}}=E\mathbf {\hat {\jmath }} \ \ \ {\vec {B}}=B\mathbf {\hat {k}} \ \ \ {\vec {v}}=v\mathbf {\hat {\imath }} \ \ \$

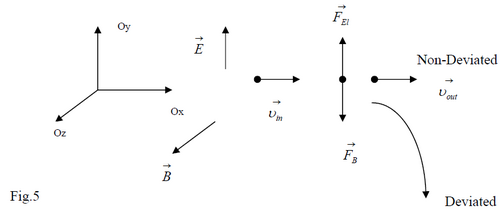
One can easily find that the electric and magnetic forces lie along the Oy axis but in opposite directions.

So, the magnitude of the net force acting on the particle is $F_{net}=qE-qvB$(9)

The special case where the net force is zero occurs for only one velocity, this happens when
$F_{net}=qE-qvB=0$(9)
The magnitude of this velocity is
$v={\frac {E}{B}}$(9)

Note that, if a parallel beam of particles with exactly this velocity enters this region, all the particles follow their original direction and are not deviated from their initial direction (Fig. 5). If the beam contains particles with different velocities, only those that fulfill the condition (9) will go out in the same direction. The others particles will deviate from their initial direction.
This is how a velocity selector works. It uses this effect to select particles with a particular velocity, determined by the chosen values of E and B.

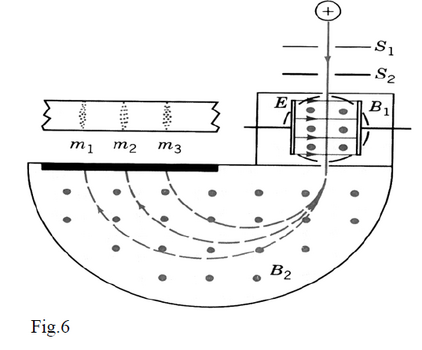
The Mass Spectrometer

The mass spectrometer is a device that contains a velocity selector and analyses the abundance of different isotopes of the same element in a sample. At first, the sample atoms are ionized (positively). Then, these charged particles (ions) are directed through a set of slits S1, S2, which collimates the beam (shapes the beam to a nice and sharp line).
This collimated beam is sent into a velocity selector ( ${\vec {E}}\perp {\vec {B}}$ ), which selects those particles with velocity $v=E/B_{1}$ . Then, the ions enter a second section where a magnetic field directed perpendicular to their velocity exerts a centripetal force
$F_{B1}=qvB_{1}=m\ a=m{\frac {v^{2}}{R}}$(11)

These ions follow circular paths with radius
$R={\frac {m}{q}}{\frac {v}{B_{2}}}={\frac {m}{q}}{\frac {E}{B_{1}B_{2}}}$(12)
As the different isotopes have different masses (but q is the same for all ions) the radius is different for each isotope and they hit the detector (photographic plate or electronic counter) at different positions. So, based on density of traces or the records’ intensity one calculates the relative abundance of different

isotopes in the sample under study . Figure 6 shows a schematic of a mass spectrometer.