Module : Torque
Kreshnik Angoni and Kevin Lenton
Torque ( given symbol ) is a measure of how much a force acting on an object causes that object to rotate, or more precisely to impart an angular acceleration.
It is super important because we use rotation frequently in our everyday lives.
For instance, the motor of your car rotates the crankshaft, which rotates the wheels. This is why we talk about the torque of car engines.
Each time you take a step your arms and legs are rotating, your muscles are applying forces to make your arms and legs turn.
Instructions on How Not to Open a Door
Think of how many doors you have opened in your lifetime...or more accurately how many doors you have rotated, because when you open or close a door you make it rotate.
Not surprisingly, doors are designed to be easy to open: they are designed to maximize the torque you apply on the door from the force you apply on the door handle. The bigger the torque applied, the easier the door is to open (the bigger the angular acceleration)
Imagine pushing a door to open it. What are the parameters that influence how easy or hard it is to open the door?
- Pivot Point
First, to rotate any object you need a pivot point. The pivot point of the door is the hinge axis: the door rotates about this point. Sometimes the pivot point is labelled O, like the origin.
- Force
Second, you need a force! The force of your push (F) causes the door to rotate about its hinges (the pivot point, O). The bigger the force, the easier it is to close the door, and the bigger the associated torque.
Next think about the position of the door handle, where you are applying the force. The door handle is almost always opposite the hinge, as far away from the hinge as possible. Let's call the distance from the hinge (pivot) to where the force is applied displacement r.
The closer the force is to the hinge (i.e. the smaller r is), the harder it is to close the door. The torque you created on the door is smaller than it would have been had you correctly pushed the handle (the handle is far away from the hinge). The bigger the distance to the pivot point, the easier it is to rotate an object; the bigger the torque.
Have you ever opened a door by pushing on the hinge?
Well, actually, if you push hard enough on the hinge the frame will collapse and the door will open. But this would be translational motion. The door will not rotate open.
Any force pushing on or through the hinge will never make any object rotate. The torque is always zero in this case (r=0). Is a force still being applied? Yes.
- Direction of the Force
When you apply a force on the handle, the force is almost always perpendicular to the door itself. Only forces (or components of forces) which are perpendicular to the door can make it open. Forces (or components of forces) parallel to the plane of the door can never make the door open: these forces are effectively pushing on the hinge (torque = zero, see above).
In summary, to maximize the ease of opening doors you need to: Have a big force acting perpendicular to the door plane and as far a distance as possible from the pivot point.
Video showing a Force opening door: Note how the torque value at the bottom changes
Now can you answer, how not to open a door while still applying a force?
Torque: Putting it together
Magnitude of the Torque
The magnitude of the torque is given by:

: the displacement vector from the pivot point to the point where force is applied,
: The force vector applied.
: the angle between and .
Note that this equation contains all the elements discussed above:
.
.
is the component of the force perpendicular to , written as
Following from this last statement, torque can also be written as:
Where
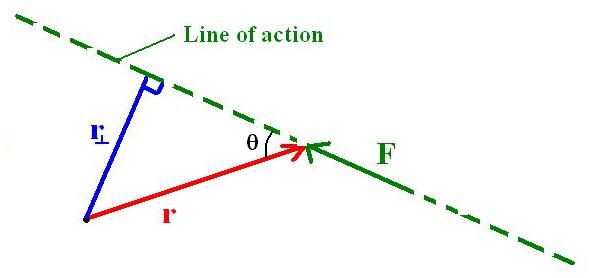
The Lever or Moment Arm
Also following from the above equation you can write the torque equation as
where
is called lever or moment arm and is the perpendicular distance between the line of action of the force and the pivot.
The line of action of a force F is the line through the point at which F is applied and along the direction in which F is applied. That is to say it is the continuation of the line the force acts through.
Cross Product Definition
All the above equations can be summed up as a cross (or vector) product. Technically, torque is the cross (or vector) product between the distance vector (the distance from the pivot point to the point where force is applied) and the force vector .
This is written as:
Units of Torque
Note that in terms of units, torque is the product of force and distance, therefore the SI unit of torque is the Newton-meter (American units are lb-ft (pound-feet)). The Work Done (or energy) also has units of Newton-meters, but is given the special unit of Joule (the unit for energy).
However, torque is not energy. So, to avoid confusion, make sure you use the units N.m, and not J, when referring to torque. The distinction arises because energy is a scalar quantity, arising from the scalar product, whereas torque is a vector, arising from the vector product of r and F.
Direction of Torque
Torque is a vector and therefore has a direction.
The direction of torque is always perpendicular to and to . Using the right hand rule (wait for your Physics NYB course if you don't know this), you can find the direction of the torque vector. If we put our right hand fingers in the direction of r, and curl them to the direction of F, then the thumb points in the direction of the torque vector.
However this course will be using special cases where the axis of rotation is given.
You will be using the following convention:
The torque is positive when the torque causes the object to rotate in the counter-clockwise direction and
The torque is negative when the torque causes the object to rotate in the clockwise direction.
SIMPLE EXAMPLE PROBLEM ON TORQUE: The Swinging Door
[OTHER EXERCISES ON TORQUE]
Misconception: Torque is Force
False
Torque is a rotational equivalent of force, but it is not force itself.
As you have seen, .
Note that the equation contains a force term, so you can use the concept of torque to find forces in your system.
Static Equilibrium
First, what does it mean for an object to be in equilibrium?
A body is at translational equilibrium if the linear acceleration of its Centre of Mass is zero ( ). That is to say
A body is at rotational equilibrium if the angular acceleration is zero ( ). That is to say
- An object is in static equilibrium if and only if and , where the net torque is the sum of all torques and the net force is the sum of all forces acting on an object.
For Static Equilibirum the object has to have zero speed (linear & angular velocities are zero)it is in static equilibrium. If it does have speed, but not acceleration (i.e. it is moving but not accelerating), then it is in dynamic equilibrium.
A note about the Centre of Mass of an Object
The weight of a body is a force that participates in all static’s problems. It appears in the conditions for
translational equilibrium and its torque appears in the condition for rotational equilibrium. Actually, the
weight of an object is the sum of all gravitation forces exerted on all the particles distributed over the body
extension. We locate this sum at the center of gravity of object. The center of gravity (CG) is the point about
which the net gravitational force exerted on body has a zero torque. It is the point at which the mass is said to act.
The position of CG is very critical for the rotational
equilibrium. How can you find the CG position?
The easiest way is to balance the object on a pivot. When the pivot is located at the centre of mass, the object will balance on the pivot.
For a uniform object, the centre of mass is right in the middle of the object.
Example Problem: The Hanging Traffic Light
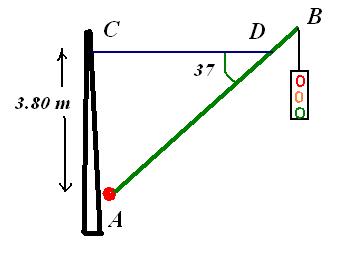
A traffic light hangs from a pole as shown in the figure. The uniform aluminum pole AB is 8 m long and has a mass of 15 kg. The mass of the traffic light is 21 kg.
a) Determine the tension in the horizontal massless cable CD.
b) Determine the horizontal and vertical components of the force exerted by the pivot A on the aluminum pole.
- To tackle the problem you have to realize that there are torques present in the situation. The forces are acting at distances from each other.
Think about what will happen if the cord is cut: the pole and traffic light will rotate about the attached point at A.
- The system is in static equilibrium: everything is stationary, so you can solve the problem by applying sum of the forces is zero, sum of the torques is zero
As previously, you will get a system of equations to solve.
- Next you should draw an Extended Body Diagram. An extended body diagram is like a free body diagram in that it shows all the forces, but at the correct distances. To find torque you need three parameters: F, r and . Remember, each force will have its own torque about the pivot point.
All these parameters should be shown on the extended body diagram for each force (and therefore for each torque). You will have to get all these parameters from information in the problem. For instance, you are told the pole is uniform, therefore its weight, which acts at its centre of mass, acts right in the middle of the pole.

- Note the coordinate system: counterclockwise torques are positive (torques only!), positive x and y are also indicated (forces only!).
- Pay attention to the forces and . These are the horizontal and vertical forces acting at the attachment point. Really there is only one force , you are splitting this up into components to fit your coordinate system. How do you know these forces are there? Imagine if there were no forces at A - that is to say the pole is not attached. What would happen? The whole system would collapse.
- Choose a pivot point for the problem. In static equilibrium you can choose any pivot point you want and solve the problem. However, some pivot points are more judicious than others. Choose pivot points where you have unknown forces. In this case you have unknown forces at A. It makes sense to choose this as your pivot point because the torque of these forces about this pivot are equal to zero. They will not appear in your torque equation. There is an unknown force of Tension T in the cable, but that is what you are looking for, so you want to keep that term in your equation.
- Just to make the point, here is a table of all the values to calculate the torques for each of the forces.
| Force | F(N) | r (m) | Torque Direction | (Nm) | |
|---|---|---|---|---|---|
| 0 | - | - | 0 | ||
| 0 | - | - | 0 | ||
| =mg=15kg*9.8 =147 | 4 m | 53 | Clockwise | -469.6 | |
| T | 37 | CounterClockwise | +3.8T | ||
| =mg=21kg*9.8 =205.8N | 8 m | 53 | Clockwise | -1314.9 |
Note that for the Tension, you could use the concept of line of action to get the same result. It doesn't matter.
Also note that according to the right hand rule, you should take the external angle between r and F. However, sin(37)=sin(180-37) (Try it if you don't believe it). Practically it does not matter which angle you choose, in either case you are finding the component of force perpendicular to r.
Now:
You can find the forces and by using the fact that for static equilibrium and therefore , .
| Axis | Sum of forces |
|---|---|
| Horizontal x | |
| Vertical y |
General Static equilibrium problem solving strategy:
- Draw an extended body diagram
- Select the coordinate system
- Determine all forces acting on an object and draw an arrow for each force indicating:
- A point where this force is applied
- In which direction this force acts
- Define a pivot point: Any pivot point will work. But to make your life easier, choose a pivot point through which unknown forces act. The torque of these forces about this pivot point will be zero.
- For each force:
- Identify the magnitude and the direction of lever arm
- Draw a diagram consisting of the force vectors, r vectors and determine the angle between these two vectors
- Determine the direction of the torque and then compute its magnitude.
- Substitute into the equation
- Compute the components of the forces
- Substitute into the equations and
- Solve the system of three equations using the method of substitution
Video Explanation+ExamplePartI