Module : Applications of Newton' Laws : Circular Motion

Kreshnik Angoni, Karen Tennenhouse and Kevin Lenton

Word Worksheet
pdfWorksheet

Learning Objectives

After reading this page, watching the videos and reviewing the exercises, you will be able to:

• Understand why uniform circular motion requires a radial force.
• Know some of the common pitfalls of circular motion dynamics.
• Apply the concepts of circular motion to some circular motion dynamics problems

THE DYNAMICS OF CIRCULAR MOTION

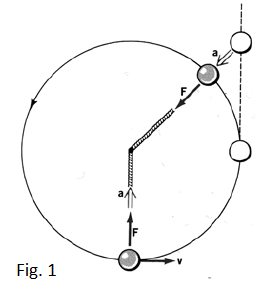
In kinematics we found that a particle moving at constant speed v around a circle with radius r has acceleration. This acceleration is directed towards the circle center at all times, and has constant magnitude:

$|{\vec {a_{c}}}|={\frac {v^{2}}{r}}$

The vector ${\vec {a_{c}}}$ is called centripetal acceleration because it is directed all times towards the circle center. The 2nd law tells that a particle with mass $m$ which is moving with centripetal acceleration is under the action of a net force directed along ${\vec {a_{c}}}$ (fig.1), that is to say towards the centre of the circle (or the negative radial axis).

$\sum {\vec {F}}_{radial}=\sum {\vec {F_{c}}}=m{\vec {a_{c}}}$ ........ (2)
That is to say the direction of the net radial force must be in the same direction as the centripetal acceleration, towards the centre of the circle.
Or:

$|\sum {\vec {F}}_{radial}|=m{\frac {v^{2}}{r}}$ ........ (3)
This force, with magnitude $m{\frac {v^{2}}{r}}$, is called centripetal force because it is directed at all times towards the circle center.
Note that it is named only from its direction and not from its physical origin.

For example, an object of mass 123 kg going around a circle of radius 10m with a velocity equal to 25m/s requires a net radial force equal to:
$|\sum {\vec {F}}_{radial}|=m{\frac {v^{2}}{r}}=123{\frac {25^{2}}{10}}=7687N$
If the force is greater than this, the object will be pulled in closer to the centre (no longer a uniform circle). If the force is smaller than this, the object will fall out of the circle.
This force could be a tension, a normal force, a weight, or a combination of different forces. The point is that the net force must be exactly that to pull the object into a circle. Also, the forces must be real physical forces in the system.

Period of the Circular Motion

The period of the circular motion is the time for the object to complete one revolution, one circle.
The distance travelled in this time is the circumference of the circle $2\pi r$.
Therefore $v={\frac {2\pi r}{T_{period}}}$.

Do not confuse $T_{period}$ with $T_{Tension}$

Misconception #1: Magical Forces

Some students think that whenever an object moves in a circle there is a magical centripetal force which should appear on their free body diagrams.
FALSE
The radial forces come from the radial forces already present in the system you are studying e.g. A force of gravity, friction, …or their sum can contribute to a centripetal force. See a fuller list here

Remember: You must not add a magical centripetal force to a free body diagram. The required radial forces come from physical forces already present..

Misconception #2: Centripetal or Centrifugal?

When you go around a circle at speed, you seem to be thrown out of the circle. Some people interpret this as a force pushing them out, a centrifugal force.
FALSE
If you think about circular motion, the forces are always pushing into the circle, that is to say pulling the object into the centre of the circle.
The reason you may think otherwise is due to the inertia of the object. Newton 1 tells us that objects want to continue at constant velocity, in a straight line. This is the tangent to the circle, in the case of circular motion. It requires a force to pull the object into the circle, so it doesn't move in a straight line.
The action of centripetal force consists of not letting the object follow its path along the tangent “as required by its inertia”.
Centrifugal effects occur as a mathematical consequence of changing your frame of reference to a non-inertial frame. This is not covered in this course.
Remember: For this course, there is no such thing as a Centrifugal force: the net radial force always pulls to the centre of the circle..

Example 1: The Conical Pendulum

A conical pendulum is a pendulum made to go around in a horizontal circle, rather than back and forth.

A mass m is swung by a string length l at an angle $\theta$ as shown. Find expressions for the speed v and the period of rotation.

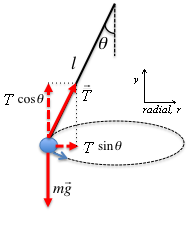
Choose your axes

First note the chosen axes. There is a vertical y axis, and a radial r axis. Positive y is up, positive r is towards the centre of the circle. Don’t forget to always define this. The radial axis in fact goes around the circle with the object, always pointing towards the centre. Therefore, the axes shown are at this point in time.
Why have you chosen these axes? You know there must be an acceleration towards the centre of the circle. Choose your axes to correspond.
There are only two forces acting on the mass: the tension, and the weight of the object. The weight is straight down: y only. Therefore it must be a component of the tension which pulls into the circle.

Equations in the y and radial directions

As before you can write equations of motion from Newton’s first and second laws in the radial and y direction. You usually solve these problems by getting one equation from axis, one equation from the other, and solving simultaneously

Equation in y direction

Equation in radial direction

$\sum F_{y}=T\cos \theta -mg=ma_{y}=0$ Note that the acceleration is zero because the mass is not moving up or down along the y axis. This is therefore an example of Newton's 1st Law. Also note that the tension is not equal to the weight of the mass. Rather $T={\frac {mg}{\cos \theta }}$

In the radial direction, there is circular motion. There must be a force pulling the mass into the circle. This force comes from the component of the tension. $\sum F_{radial}=T\sin \theta$ Note that there is a net force, therefore the system is not in equilibrium. =Newton's 2 Law Now this radial force gives rise to radial acceleration. Therefore: $\sum F_{radial}=T\sin \theta =ma_{centripetal}=m{\frac {v^{2}}{r}}$ Rearranging: $v^{2}={\frac {rT\sin \theta }{m}}$

Resolve the Equations

As in many Newton2 problems, you take an equation from one axis and substitute it into the other axis and solve for what you are looking for. In this case, let's find an expression for the speed of the mass going around, and the period of rotation.

Substitute in the expression for T from the y axis, into the radial equation.
$v={\sqrt {{\frac {r}{m}}({\frac {mg}{\cos \theta }})\sin \theta }}={\sqrt {\frac {rg\sin \theta }{\cos \theta }}}$
Rather than r we would like an expression in $l$ so we sub in $r=l\sin \theta$

$v={\sqrt {\frac {lg\sin ^{2}\theta }{\cos \theta }}}$

The period of rotation, also sometimes labelled T is given by:

$T_{period}={\frac {2\pi r}{v}}=2\pi l\sin \theta {\sqrt {\frac {\cos \theta }{lg\sin ^{2}\theta }}}=2\pi {\sqrt {\frac {l\cos \theta }{g}}}$

!!!!Note: This equation only applies to the specific case of the conical pendulum. It is not a general equation for all pendula. What you need to remember is the strategy for solving circular motion problems!!!!

Example 2: Car going around a bend in the road

A car travels at high speed around a horizontal curved path of radius r.
The coefficient of static friction between the tires and the road is $\mu _{s}$
The coefficient of kinetic friction between the tires and the road is $\mu _{k}$
Find the maximum speed that the car can go around the circle.

First visualize the problem:

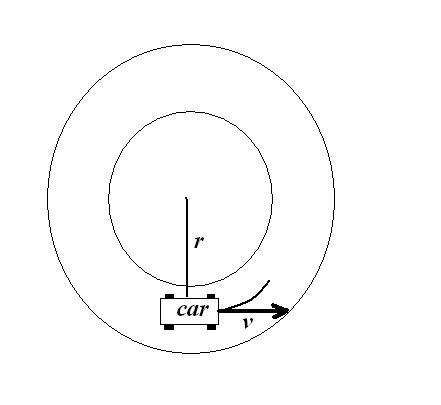
The car is going around at constant speed. However, the velocity vector is tangential to the circle at any particular point.
How does friction affect the car?
You can test how friction affects the system by thinking about how the car will react if the road is covered in ice (i.e. no friction)
The car will go straight (Newton 1)!
Therefore it is the force of friction which keeps the car in the circle.
But what sort of friction is it? The tires are not spinning on the road. Therefore the rubber tire surface is static relative to the road surface. It is the force of static friction acting here.
The net force must be radial pulling the car into the circle.

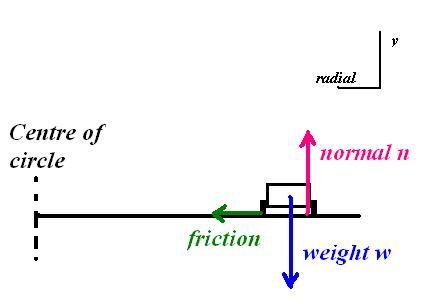
Choose your axes

First note the chosen axes. There is a vertical y axis, and a radial r axis. Positive y is up, positive r is towards the centre of the circle. Don’t forget to always define this. The radial axis in fact goes around the circle with the car, always pointing towards the centre. Therefore, the axes shown are at this one point in time.
Why have you chosen these axes? You know there must be an acceleration towards the centre of the circle. Choose your axes to correspond.
There are only three forces acting on the mass: the force of friction, the normal, and the weight of the object. The weight and normal force are straight down: y only. Therefore it must be the force of friction which pulls into the circle.

Equations in the y and radial directions

As before you can write equations of motion from Newton’s first and second laws in the radial and y direction. You usually solve these problems by getting one equation from axis, one equation from the other, and solving simultaneously

Equation in y direction

Equation in radial direction

$\sum F_{y}=n-mg=ma_{y}=0$ Note that the acceleration is zero because the car is not moving up or down along the y axis. This is therefore an example of Newton's 1st Law. $\therefore n=mg$

In the radial direction, there is circular motion. There must be a force pulling the mass into the circle. This force comes from the force of friction. $\sum F_{radial}=F_{friction}$ We are asked for the max speed, therefore we want the max force of static friction. $F_{friction_{max}}=\mu _{s}n$ Note that there is a net force, therefore the system is not in equilibrium. =Newton's 2 Law Now this radial force gives rise to radial acceleration. Therefore: $\sum F_{radial}=\mu _{s}n=ma_{centripetal}=m{\frac {v^{2}}{r}}$ Rearranging: $v^{2}={\frac {r\mu _{s}n}{m}}$

Resolve the Equations

As in many Newton2 problems, you take an equation from one axis and substitute it into the other axis and solve for what you are looking for. In this case, let's find an expression for the speed of the car going around, and the period of rotation.

Substitute in the expression for n from the y axis, into the radial equation.
$v_{max}={\sqrt {{\frac {r}{m}}(\mu _{s}mg)}}={\sqrt {r\mu _{s}g)}}$

Say r = 157 m, $\mu _{s}=0.5$, then the max velocity is 28 m/s. Note that it is independent of mass.

What happens if you go faster then this?
The force of friction cannot provide the necessary centripetal force. The car will slip off the road.
What happens if you go slower than this?
The force of static friction will exactly provide the force required to get the car around the bend.
Video Explanation

Example 3: Vertical Circle

The classic case of a vertical circle is a car going over a hill and through a valley. We are most interested in the special cases of just at the bottom of the valley and just at the top of the hill. Other examples of a vertical circle are a ball on a string being swung in a vertical circle and a person going around on a Ferris wheel (la grande roue).
For the car, the only forces acting on it are the normal force from the road and the weight. Only these forces can contribute to pulling the car into a circle.

First visualize the problem:

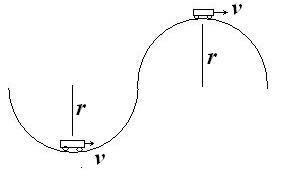
The car is going around at constant speed. However, the velocity vector is tangential to the circle at any particular point.
We can start by looking at the special case of the car down in the valley.
The net force must be radial pulling the car into the circle. The centre of the circle is up, so the acceleration is up and the net force is up. Therefore the normal force must be greater than the weight.

Choose your axes

First note the chosen axes. There is a horizontal x axis, and a radial r axis. Positive r is up towards the centre of the circle, positive x is right. Don’t forget to always define this. The radial axis in fact goes around the circle with the car, always pointing towards the centre. Therefore, the axes shown are at this point in time.
Why have you chosen these axes? You know there must be an acceleration towards the centre of the circle. Choose your axes to correspond.
There are only two forces acting on the mass: the normal, and the weight of the object. The weight and normal force are straight up and down: r (or y if you insist) only.

Equations in the y and radial directions

As before you can write equations of motion from Newton’s first and second laws in the radial and y direction. You usually solve these problems by getting one equation from axis, one equation from the other, and solving simultaneously

Equation in x direction

Equation in radial (or y) direction

$\sum F_{x}=0$ Note that the acceleration is zero because the car is not accelerating along the x axis. This is therefore an example of Newton's 1st Law.

In the radial y direction, there is circular motion. There must be a force pulling the mass into the circle. This force comes from the combination of the normal and weight. $\sum F_{radial}=n-w$ Note that there is a net force, therefore the system is not in equilibrium. =Newton's 2 Law Now this radial force gives rise to radial acceleration. Therefore: $\sum F_{radial}=n-mg=ma_{centripetal}=m{\frac {v^{2}}{r}}$ Rearranging: $v^{2}={\frac {r(n-mg)}{m}}$

Resolve the Equations

As in many Newton2 problems, you take an equation from one axis and substitute it into the other axis and solve for what you are looking for. In this case, you only have one equation. A common question is to find the normal force.

Rearrange the equation for n.
$n={\frac {v^{2}m}{r}}+mg$

Note that the normal force is not equal to mg in this case. It is always greater than mg because there must be a net force up.

Can you find an expression for the normal force at the top of the hill?
Video Solution of this question