Module 5: 2D Projectile Motion

Helena Dedic, Kreshnik Angoni and Kevin Lenton

Module 2D Motion Worksheet.docx
Module 2D Motion Worksheet.pdf

Learning Objectives

After reading this page, watching the videos and reviewing the exercises, you will be able to:

• Understand 3D (2D) motion as the vector combination of motion along 3(2) 1D-Independent axes. What links the axes is time.
• Understand Projectile motion as a special case of 2D motion with a constant acceleration in one axis, and no acceleration in the other.
• Describe the independence of horizontal and vertical components of motion.
• Predict the landing point of a projectile, given the initial conditions

Extending the 1D case to 2 and 3 Dimensions

1D Motion: Choose an Axis which corresponds to the Straight Line Motion

When a path of a particle is a straight line we say that its motion is one dimensional. In such cases we orient one of the axis along the path traveled by the particle and we can describe its position or velocity by one of the components:

2D Motion: Vector Sum of 1D Coordinates

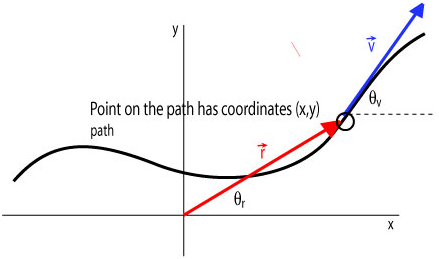
Now consider when the path of a particle is a curve in a plane (let's say either the horizontal or vertical plane) then we say that its motion is a two dimensional 2D motion. The Figure shows the y vs x graph (not y vs t!).

The position vector at any instant t has two components each of which is a function of time.

${\vec {r}}(t)=x(t){\hat {i}}+y(t){\hat {j}}$

The velocity vector points in the direction of the tangent to the path. We cannot deduce its magnitude because we do not have any time information at the moment, but we know that it has two components neither of which is zero at t:

${\vec {v}}(t)=v_{x}(t){\hat {i}}+v_{y}(t){\hat {j}}$

If you knew the components of the velocity vector ${\vec {v}}(t)$, how could you calculate the magnitude of the velocity (otherwise known as the speed)?
$\Rightarrow \ \ |{\vec {v}}(t)|={\sqrt {v_{x}(t)^{2}i+v_{y}(t)^{2}}}$

The acceleration vector also has two components. We cannot deduce either the direction or its magnitude from the diagram above. But if we knew then, we could write:

${\vec {a}}(t)=a_{x}(t){\hat {i}}+a_{y}(t){\hat {j}}$

In this course you will study two cases of two-dimensional motion: projectile motion and motion with constant acceleration. This module looks exclusively at Projectile Motion.

Equations of Motion in 3D

The $x,y,z$ axes are independent of each other because they are orthogonal (at 90 degrees to each other). Therefore what is important to remember is that the motion along the horizontal (x) axis does not affect the motion along the vertical axis and vice-versa. Horizontal motion and vertical motion are totally independent of each other.
This means that you can rewrite the equations of motion independently for each axis. What links the axes at a particular point in the motion is time.

	X Axis	Y Axis	Z Axis
Equation 1	$v_{f_{x}}=v_{i_{x}}+a_{x}t$	$v_{f_{y}}=v_{i_{y}}+a_{y}t$	$v_{f_{z}}=v_{i_{z}}+a_{z}t$
Equation 2	$x_{f}-x_{i}=v_{i_{x}}t+{\frac {1}{2}}a_{x}t^{2}$	$y_{f}-y_{i}=v_{i_{y}}t+{\frac {1}{2}}a_{y}t^{2}$	$z_{f}-z_{i}=v_{i_{z}}t+{\frac {1}{2}}a_{z}t^{2}$
Equation 3	$v_{f_{x}}^{2}=v_{i_{x}}^{2}+2a(x_{f}-x_{i})$	$v_{f_{y}}^{2}=v_{i_{y}}^{2}+2a(y_{f}-y_{i})$	$v_{f_{z}}^{2}=v_{i_{z}}^{2}+2a(z_{f}-z_{i})$
Equation 4	$(x_{f}-x_{i})=+{\frac {1}{2}}(v_{f_{x}}+v_{i_{x}})t$	$(y_{f}-y_{i})=+{\frac {1}{2}}(v_{f_{y}}+v_{i_{y}})t$	$(z_{f}-z_{i})=+{\frac {1}{2}}(v_{f_{z}}+v_{i_{z}})t$

Projectile Motion: A special case

Note: Using axes where up is positive y, and to the right positive x.

A particle is in projectile motion when:
1. It has a horizontal component of velocity (i.e. $v_{x}\neq 0$ ; $v_{x}$ is different from zero) and
2. The force of gravity is the only force acting on it. This means you are ignoring other forces such as air resistance (you suck all the air out of the problem), and you therefore only have one acceleration, g in the negative y direction ($-{\hat {j}}$).
You are saying the acceleration in the x direction is zero $a_{x}=0$ and the acceleration in the y direction is -9.8 m/s/s $a_{y}=-9.8ms^{-2}$.
The implication of $a_{x}=0$ is that, in the x direction, the velocity does not change and the only equation you need to describe the motion is essentially $speed={\frac {distance}{time}}$

More correctly, the kinematic equations can be rewritten for this case of $a_{x}=0$ and $a_{y}=-g$:

	X Axis	Y Axis
Equation 1	$v_{f_{x}}=v_{i_{x}}$	$v_{f_{y}}=v_{i_{y}}+(-g)t$
Equation 2	$x_{f}-x_{i}=v_{i_{x}}t$	$y_{f}-y_{i}=v_{i_{y}}t+{\frac {1}{2}}(-g)t^{2}$
Equation 3	$v_{f_{x}}^{2}=v_{i_{x}}^{2}$	$v_{f_{y}}^{2}=v_{i_{y}}^{2}+2(-g)(y_{f}-y_{i})$
Equation 4	$(x_{f}-x_{i})=+{\frac {1}{2}}(v_{f_{x}}+v_{i_{x}})t$	$(y_{f}-y_{i})=+{\frac {1}{2}}(v_{f_{y}}+v_{i_{y}})t$

If you think about throwing a ball, you can always align your x axis to follow the shadow (projection) of the ball. This means you only need 2D to describe projectile motion. We do not consider a z axis.
As usual, the axes are always independent. Time is the parameter which links the axes.

Derivation of the Equation for Horizontal Range

You are throwing a ball with initial velocity of magnitude $v_{i}$ and direction $\theta$ above the horizontal. You are asked to calculate the Horizontal Range. The Range is a special term for the x displacement when the ball comes down to the same level from which it is thrown. That is to say $\Delta y(t)=0$.

Projectile Motion

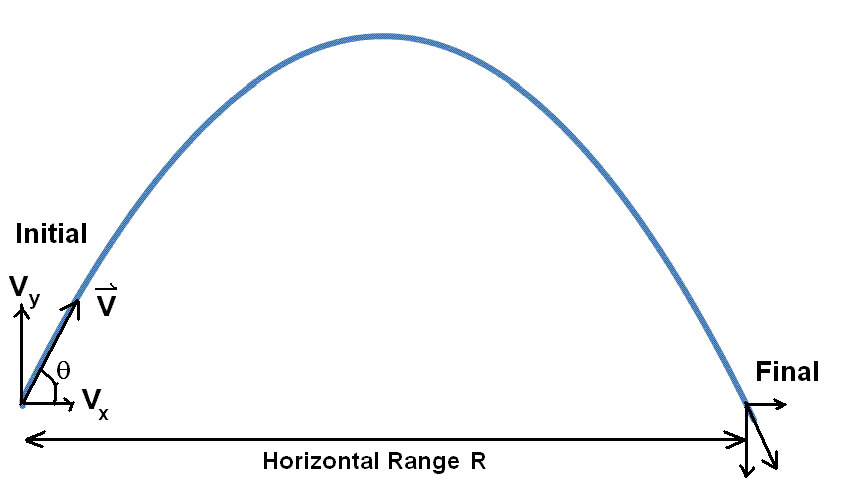
Then the x and y components of the initial velocity are:

$v_{i_{x}}=v_{i}cos\theta$
$v_{i_{y}}=v_{i}sin\theta$

We also note that $\Delta x(t)=R$, =the horizontal Range; and $\Delta y(t)=0$. We will substitute these values into the equations of kinematics for projectile motion.
First you can create a table of all the information you have and what you are looking for, with x and y separated out (because they are independent).

Parameter	Values for Horizontal (X) Axis	Values for Vertical (Y) Axis
Displacement $\Delta d$	$\Delta x=R=?$	$\Delta y=0m$
$v_{i}$	$v_{i_{x}}=v_{i}cos\theta$	$v_{i_{y}}=v_{i}sin\theta$
$v_{f}$	$v_{f_{x}}=v_{i}cos\theta$	$v_{f_{y}}=?$
$a$	$a_{x}=0ms^{-2}$	$a_{y}=-g$
$t$	$t=?$

You are looking for something along the x axis, R, so find an expression for time using the y axis.
The equation you should use is:
$y_{f}-y_{i}=v_{i_{y}}t+{\frac {1}{2}}a_{y}t^{2}$
Substituting in from the above table:
$0=v_{i}(sin\theta )t+{\frac {1}{2}}(-g)t^{2}$
Isolate t :

$0=v_{i}(sin\theta )t-{\frac {g}{2}}t^{2}$
The roots are $t={\frac {2v_{i}sin\theta }{g}}$ and $t=0$.
The $t=0$ root corresponds to the initial conditions.

Now in the x direction the only equation you need is:
$x_{f}-x_{i}=v_{i_{x}}t$
Therefore, $R=v_{i}(cos\theta )t$

and substitute for t :

$R=v_{i}(cos\theta ){\frac {2v_{i}sin\theta }{g}}={\frac {2v_{i}^{2}sin\theta cos\theta }{g}}$
Almost there!
You are going to manipulate this equation into a slightly different form to get some interesting conclusions.
We note the trigonometric identity:

$sin2\theta =2sin\theta cos\theta$.

You can substitute for $sin\theta cos\theta$ in the equation for the range and obtain:

$R={\frac {2v_{i}^{2}sin2\theta /2}{g}}={\frac {v_{i}^{2}sin2\theta }{g}}$

So, in general:

$R={\frac {v_{i}^{2}sin2\theta }{g}}$



!!!!Be very careful with this equation: It can only be used when the y displacement is zero, that is to say the object comes back to the initial y position!!!

For what angle is R maximum?
That will occur when $sin2\theta =1$
or rather when $2\theta =90^{\circ }$
or rather when
$\theta =45^{\circ }$

This means to maximize the range of a ball throw, you should throw it at an angle equal to $\theta =45^{\circ }$.
Also look at the velocity term $v_{i}^{2}$. It is a square relationship. So by increasing $v_{i}$ you increase R by alot. But you probably knew that already!
How does g affect the range? How far would your ball go on the moon, all the other parameters held constant?

See how this plays out in the following video. Pay attention to the 45 degree case.

Range of Projectile

See how the horizontal range of a projectile depends on the initial angle of incidence. The initial velocity is the same in each case.

Solving Projectile Motion Problems

Projectile problems are easily solved if you stick to a logical procedure. Your very first task is to separate the motion into x (horizontal) and y (vertical) parts (because they are independent). The problems are almost always solved in two parts, one involving horizontal motion, the other involving vertical motion.
The part you attack first depends upon the particular problem you are solving. But in general if you are asked to find a parameter on the horizontal axis, e.g. the horizontal displacement, you should start with the vertical to find a value, or an expression for the time (using the equation of motion for that axis), and then substitute into the equation of motion for the other axis.
To repeat: The general procedure is that you use one of the independent motions (horizontal or vertical) to find the time in flight, then use that time to determine the parameter of interest in the other axis.

Video of Problem Solving Strategy

Video of Problem Solving Strategy
Note in this example, the object is going straight off the cliff. In this case the initial y velocity is zero.

More Problem Solving Strategy
This video is quite detailed. One thing that this person recommends is to split problems up into up and down sections- to avoid quadratic equations. Do not show this fear!

Exercises on Projectile Motion

Exercises on Projectile Motion