Module 4: Equations of Motion for Constant Acceleration

Helena Dedic, Kreshnik Angoni and Kevin Lenton

Finding the velocity by taking the slope of an x vs t graph or the area under the curve on an a vs t graph is interesting but when the graphs are not straight lines (which is most of the time) and one looks for the instantaneous velocity of many points, the procedure becomes cumbersome and complicated. In these situations, analytical methods provide the result in the form of equations and their solutions as functions. By using a function one can find quickly the required quantity value for any moment of time.
For the special case of constant acceleration, the Equations of Motion exactly describe the motion in terms of position, velocity and acceleration.
These equations are really vector equations, and therefore you need to be ultra careful about the sign of the parameters (remember sign indicates direction).

Here are the four kinematic equations:

Equation 1	$v_{f}=v_{i}+at$
Equation 2	$x_{f}-x_{i}=v_{i}t+{\frac {1}{2}}at^{2}$
Equation 3	$v_{f}^{2}=v_{i}^{2}+2a(x_{f}-x_{i})$
Equation 4	$(x_{f}-x_{i})=+{\frac {1}{2}}(v_{f}+v_{i})t$

Derivation of Equations of Motion

Video showing derivations below

Equation 1

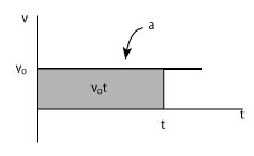
Consider a v-t graph for an object moving with constant velocity.
Motion with constant velocity implies that the acceleration is equal to zero and therefore the v - t graph is a horizontal line.
$v(t)=v_{o}$

The displacement is the area under the v - t graph

We write $\Delta x(t)=v_{o}t$

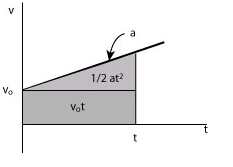
Motion with constant acceleration implies that the velocity is a linear function of time. Given that the initial velocity is $v_{0}$ we can write

$v(t)=v_{o}+at$

where the acceleration is the slope of the graph and $v_{o}$ is the intercept.
This equation is sometimes written as:

$v_{f}=v_{i}+at$

Equation 2

The displacement is the area under the v - t graph

We write

$\Delta x(t)=v_{o}t+{\frac {1}{2}}at^{2}$
The displacement in both cases is $\Delta x(t)=x(t)-x_{o}$

Therefore:

$x_{f}-x_{i}=v_{i}t+{\frac {1}{2}}at^{2}$

Equation 3

There are two independent equations describing motion with constant acceleration and five variables: $\Delta x(t)$, v(t), $v_{0}$, a and t. Consequently, in any problem we can solve for two of those variables and three other must be given.

We can derive another useful equation by eliminating t from the two equations above.

We begin with Equation 1:

$v(t)=v_{o}+at$

We isolate t:

$t={\frac {v(t)-v_{o}}{a}}$

Then we substitute for t in the equation for the displacement:

$\Delta x(t)=v_{o}\left({\frac {v(t)-v_{o}}{a}}\right)+{\frac {1}{2}}a\left({\frac {v(t)-v_{o}}{a}}\right)^{2}$

We will now multiply both sides by 2a. This step will eliminate fractions from this equation.

$2a\Delta x(t)=2av_{o}\left({\frac {v(t)-v_{o}}{a}}\right)+2a{\frac {1}{2}}a\left({\frac {v(t)-v_{o}}{a}}\right)^{2}$

This leads to:

$2a\Delta x(t)=2v_{o}(v(t)-v_{o})+(v(t)-v_{o})^{2}$

Expanding:

$2a\Delta x(t)=2v_{o}v(t)-2v_{o}^{2}+v^{2}(t)+v_{o}^{2}-2v_{o}v(t)$

which leads to:

$2a\Delta x(t)=-v_{o}^{2}+v^{2}(t)$

This can finally be written in the form:

$v^{2}(t)=v_{o}^{2}+2a\Delta x(t)$ or

$v_{f}^{2}(t)=v_{i}^{2}+2a(x_{f}-x_{i})$

Equation 4

The forth equation, which is often quoted, is simply a combination of Equation 1 and Equation 3 (and is therefore redundant).
Starting with Equation 3:
$v_{f}^{2}=v_{i}^{2}+2a(x_{f}-x_{i})$
Rearrange Equation 1 to isolate a:
$v_{f}=v_{i}+at\ \ \ \Rightarrow \ \ \ a=({\frac {v_{f}-v_{i}}{t}})$
Substitute a into Equation 3:
$v_{f}^{2}=v_{i}^{2}+2({\frac {v_{f}-v_{i}}{t}})(x_{f}-x_{i})$
$v_{f}^{2}-v_{i}^{2}=+2({\frac {v_{f}-v_{i}}{t}})(x_{f}-x_{i})$
Expand the left hand side:
$(v_{f}-v_{i})(v_{f}+v_{i})=+2({\frac {v_{f}-v_{i}}{t}})(x_{f}-x_{i})$

Divide both sides by $(v_{f}-v_{i})$ giving
$(v_{f}+v_{i})=+2({\frac {x_{f}-x_{i}}{t}})$

Or:

$(x_{f}-x_{i})=+{\frac {1}{2}}(v_{f}+v_{i})t)$

Exercises

How to list variables when problem solving.
Continuation of above.

How to pick the right equation

Drag Race Style Problems

You are invited to review some of these problems. Excercise 2 does not use the kinematic equations of motion, but is a good review.

FreeFall: A special case of Constant Acceleration

Helena Dedic

A particle is in a free fall if the gravitational force is the only force acting on it. Note that:

a. the acceleration is equal to g pointing vertically down;

b. we will use $g=9.8m/s^{2}$;

c. we will almost always choose the positive axis pointing upward and therefore the y-component of the acceleration is always $a_{y}=-9.8m/s^{2}$;

d. the velocity is falling at a rate of 9.8 m/s every second: e.g., knowing that the velocity is 50 m/s at some time t we can say that 1 s later it will 40.2 m/s, 5 s later it will be 1 m/s etc.;

e. a particle is in a free fall (regardless of whether the direction of motion is upward or downward) only if it has no contact with other particles.

Consider an example of a "ball" tossed up: the ball is initially held at rest by the hand; then the hand flips upward and the ball gain upward velocity and at some point fly up in the air, rise to the maximum height, fall down and get caught by the hand coming to rest. Study the diagram and the v - t graph of this event.

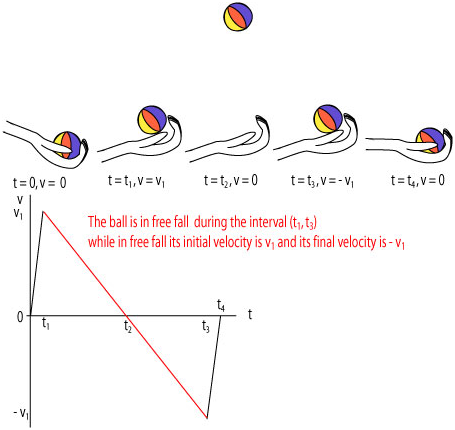
• The equations of kinematics for objects in free fall become:

$v_{y}(t)=v_{y0}+(-9.8)t$

$\Delta y(t)=v_{y0}(t)+{\frac {1}{2}}(-9.8)t^{2}$

$v_{y}^{2}(t)=v_{y0}^{2}+2(-9.8)\Delta y(t)$

• Problem solving strategy is similar to the one we used for motion with constant acceleration. Use the following tips when thinking about problems:

o the downward displacement is negative;

o initial velocity is not zero unless an object is dropped (released);

o final velocity is not zero unless we inquire about maximum height;

o final velocity is negative if an object is moving downward.

• The velocity is a linear function and therefore the change of velocity is proportional to time interval e.g., doubling the time interval makes the change of velocity double.

• The displacements is a quadratic function of time. It has a linear term $v_{0}$t and a quadratic term ½a$t^{2}$. It means that the displacement is not proportional to time:

o Displacement during two equal intervals of time are not equal.

o When displacements are equal then the time intervals are not equal.

• TOP

Exercises

• [on Free Fall Motion]