Module 2: Intro to Vectors
Michael Cowan, Helena Dedic, Dave Oram and Kevin Lenton
Vector Worksheet.docx
Vector Worksheet.pdf
Have you ever thought about sending a rocket to the moon?
Not only do you have to think about the speed of the earth, of your rocket, of the moon, but you have to work out the direction each of these objects is traveling, if your rocket is going to meet up with the moon.
In fact there are many useful and important quantities which have a direction that we cannot ignore. Such quantities are called vectors. Vectors always have a value (magnitude) and direction. You always have to take the direction of a vector into account when manipulating them
There are also many quantities which do not have a direction, and which add according to the ordinary rules of arithmetic. Such quantities are called scalars.
Examples of Vectors and Scalars
| Scalar | Vector |
|---|---|
| distance | Displacement |
| speed | Velocity |
| Acceleration | |
| Force | |
| Momentum |
Note that we often use Vector names as scalars e.g. acceleration, where we just quote the magnitude of the acceleration without giving the direction. Technically this is an incorrect usage.
Breakdown of a Vector
There are always three aspects to any vector: the sign, the magnitude and the direction
| + or - | magnitude (+units) | direction |
|---|---|---|
| The sign gives either forward of reverse along the axes, and is really therefore part of the direction | The magnitude is always positive (absolute value), and gives the value of the vector | Direction gives the direction! Could be an angle or an axis indication |
For instance, +3m on the line from the origin to the door is a vector.
The measurement is 3m is a scalar, because there is no indication of direction (including no sign).
Note that scalars do not have direction and therefore only have absolute value magnitudes.
Algebraic Representation of Vectors
Helena Dedic
It is important that you learn to use symbols for vector, magnitude of a vector and component of a vector. Further, it is important to use these symbols when appropriate. In different texts or in different domains (e.g., physics, linear algebra etc.) these symbols may vary and you should be prepared to recognize different conventions. In your textbook and on this site the symbols are in the first row. The second row shows alternative symbols that physics texts often use. The third row shows the symbols for the same concepts that you will learn in linear algebra.
domain vector magnitude component physics A A physics A linear algebra
Be aware that it is incorrect to write an equation like this one:
This is because one side of the equation is a vector, the right side of the equation is a scalar!
But it is correct to write :
because there is no direction on the left (a scalar) and there is a scalar on the other side too.
From now on we will show vector quantities in boldface type (see the symbols in the lists above), whereas scalars will be printed normally.
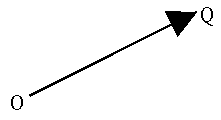
Graphically, a vector is represented by an arrow, defining the direction, and the length of the arrow defines the vector's magnitude. This is shown in the diagram . If we denote one end of the arrow by the origin O and the tip of the arrow by Q. Then the vector may be represented algebraically by OQ.
Properties of Vectors
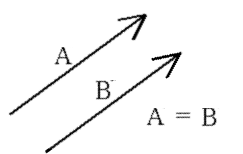
Equality
Two vectors, A and B are equal if they have the same magnitude and direction, regardless of whether they have the same initial points. This is important because it means you can move vectors around, and if they keep the same magnitude and direction, they are the same!
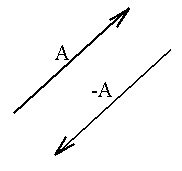
A vector having the same magnitude as A but in the opposite direction to A is denoted by -A
Vector Addition and Subtraction
The world would be a simpler place if all physical quantities were scalars, and added according to the ordinaiy rules of arithmetic e.g. 6 kg + 8 kg = 14 kg. However, two displacements, of
magnitude 6 km and 8 km, can add together to give anything from 2 km to 14 km. It all depends
on their directions.
ADDING VECTORS GRAPHICALLY
We can now define vector addition. The sum of two vectors, A and B, is a vector C, which is obtained by placing the initial point of B on the final point of A, and then drawing a line from the initial point of A to the final point of B , as illustrated in Panel 4. This is sometines referred to as the "Tip-to-Tail" method. We can add any two (or more) vectors graphically in much the same
way:
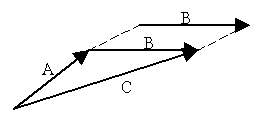
a) Represent the first vector by an arrow in the correct direction, drawn to scale i.e. with the
length of the arrow proportional to the magnitude of the vector.
b) The arrows can be placed anywhere on the page as long as they point in the proper direc-
tion. Think of each arrow as carrying its own portable compass. Start the second arrow
with its tail at the head of the first arrow; point it in its proper direction, and draw it to the
same scale as the first.
c) Continue with any further vectors, adding arrows tail-to-head one at a time.
d) The resultant (vector sum) is represented by an arrow which goes directly from the tail of
the first arrow to the head of the last. Draw this on your diagram.
e) Use a ruler and a protractor to measure the length of your resultant, and its direction relative to some standard axis. Use the scale of your diagram to convert the length to the ac-
tual magnitude.
Your resultant vector is where you begin to where you end.
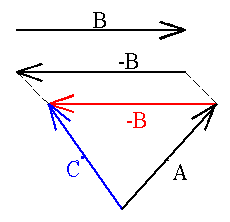
SUBTRACTING VECTORS GRAPHICALLY
Vector subtraction is defined in the following way. The difference of two vectors, A - B , is a vector C that is, C = A - B
or C = A + (-B).Thus vector subtraction can be represented as a vector addition.
The graphical representation is shown in Panel 5. Inspection of the graphical representation shows that we place the initial point of the vector -B on the final point the vector A , and then draw a line from the initial point of A to the final point of -B to give the difference C.
This is also known as the displacement of two vectors: and gives the vector between the arrow heads of each vector
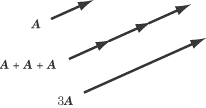
MULTIPLYING A VECTOR BY A SCALAR
All that happens when you multiply by a scalar is that the magnitude of the vector is multiplied by this number, the direction does not change. Similarly, division by a scalar, reduced the magnitude by the factor, but does not change the direction
Coordinate Systems
There are two coordinate systems that you should be concerned with:
Cartesian, and Spherical-Polar.
Note that for any coordinate system the coordinate axes are orthogonal (meaning at right angles to each other) and therefore are independent.
The most important aspect of any coordinate system is that the axes are independent.
A description of these coordinate systems in 2D
Basically Cartesian coordinates consist of an origin and an x,y coordinate.
Spherical polar consists of the length r from the origin, and an angle .
The x, and y coordinates like this are called the coordinates. When they refer to a vector, they are referred to as components.
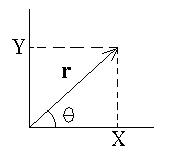
Converting between Coordinate Systems 2D
x,y, in terms of r and
r,, in terms of x and y
From Pythagoras:
Note that this allows use to calculate the length (or magnitude) of any vector for which you know the x and y components.
and
Careful with your signs!!!!
Be very careful when you are calculating your components.
If your vector is in the second, third or forth quadrant, then the components can be negative.
Unit Vectors
Unit means 1, and any unit vector has a magnitude = 1. Unit vectors are used to indicate the direction of a vector alone.
A unit vector is sometimes denoted by a hat over the vector.
e.g. is the unit vector for vector
Definition of a unit vector
You can find the Unit vector of any vector by dividing the vector by its magnitude.
(pronounced i hat, j hat) Notation
Unit vectors are very useful, particularly when they are defined along our principle axes x,y (and z). Unit vectors along these axes are given special names.
A unit vector along the x direction is called
A unit vector along the y direction is called
A unit vector along the z direction is called
This means we can express any vector as the sum of vectors along the axes.
Remember, your vector is from where you begin to where you end. What you are doing here is breaking your vector down into the sum of vectors along the axes. This makes your life easier because, when you are adding a whole bunch of vectors together, you can simply combine all the vectors along the x, y and z axes separately.
Adding vectors by components example
Example:
Take two vectors A and B. They can be broken up into the sum of vectors along the axes, having lengths equal to the components.
Let's add the two vectors together:
You can combine the vectors which are in the same direction. i.e. everything in the x or direction, everything in the y or direction etc.
e.g.
Where the components are:
The magnitude is given by:
Note I am trying to confuse you here! This is the magnitude of a 3D vector.