Magnetic Forces and Fields

  Chapter 9 Notes: Magnetic Forces and Magnetic Fields 

Do currents exert forces on each other in the same way that charges do?
Our study of electric forces and electric fields began with a simple experimental observation: charged particles exert forces on each other. From that, we were able to deduce that a charged particle creates an “alteration” in space, and that alteration [which we called the electric field] exerts a force on any other charged particle that is placed in its presence. We found that the force exerted by one charge on another gets smaller as their separation increases, but that the force gets larger as the charge amount increases.
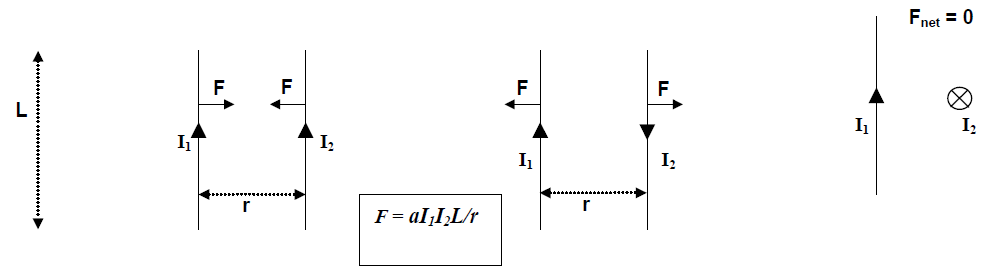
Another simple experimental observation leads to another whole set of physical phenomena. It is relatively easy to observe that two current-carrying conductors will exert forces on each other, even though the conductors do not have any net charge. Since they are not charged positively or negatively, this new force can not be the same as the electrical force we investigated earlier. This new force is due to the influence of moving charges on each other. If one has two very long conducting wires of length L placed parallel to each other, carrying currents I1 and I2 separated by a distance r, it is found that the magnitude of the mutual force exerted by one wire on the other is given by F = aI1I2L/r, where a is a proportionality constant. If the currents flow in the same direction, the force is attractive. If they flow in opposite directions, the force is repulsive. It is also observed that if one wire is rotated about its center point until it is perpendicular to the other, there is no net force on it at all!

In a way that is similar to our previous analysis of electric forces and fields, one can define a physical entity called the “magnetic field” [symbol: B; unit: T (tesla)] that is produced by any current-carrying conductor. This magnetic field is a vector quantity: it has both magnitude and direction. For a long straight wire, the magnitude of this field depends on the distance r from the wire, and is given by B = aI/r, where the same constant a appears as before.
Just as with the analysis of electric fields, we are often interested in the effect of the magnetic field on some “test” current, and are not interested in (or have no information about) the source currents that produced the magnetic field. If a test current consisting of a straight wire of length L carrying current I is placed in a uniform external magnetic field B, then the magnitude of the force F exerted on that wire is given by F = BIL sin, where  is the angle between the direction of the magnetic field, and the direction in which the current is flowing. (An “external” magnetic field is one that is produced by source currents outside of the region in which we are interested; we usually don’t have any information about those source currents. However, if the source current is just a long straight wire, it is relatively easy to analyze both the field produced by that source current, and the forces exerted by its magnetic field on some other straight wire that is parallel to it.)
For our purposes, we may always choose the angle  to lie between 0 and 180. Then, the magnetic force on a current will be at a maximum when the current flows perpendicular to the direction of the magnetic field ( = 90). When the current flows in the same ( = 0) or opposite ( = 180) direction as the magnetic field, the magnetic force on that current will be zero.
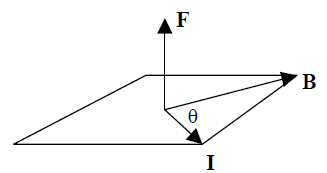
Experiments show that the direction of the force experienced by a current placed in a magnetic field is perpendicular to the direction of the current. Moreover, the direction of the force is also perpendicular to the direction of the magnetic field. This implies that the force vector is perpendicular to the plane formed by the magnetic field and the current. But there are two possible directions perpendicular to a plane – how do we choose?
This brings us to a particularly difficult aspect of magnetic fields: that of determining the direction of the field, or of the force it produces. To do this it is convenient to use two different so-called “right-hand rules.”
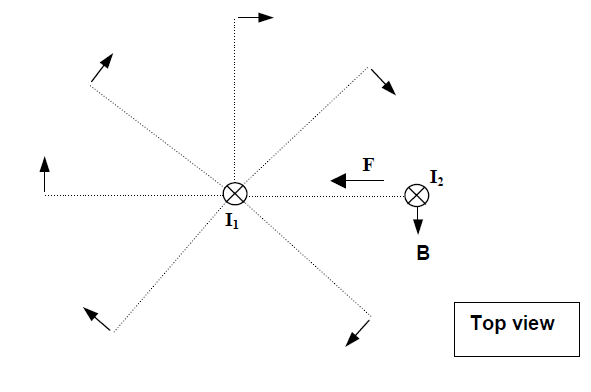
1) To find the direction of the magnetic field produced by current flowing in a long straight wire at a point P in space near the wire, draw a straight line from the wire to that point as shown in the top view below. (In this example, the current is flowing into the page.) The magnetic field points perpendicular to that line, and is in the plane perpendicular to the wire (here, the plane defined by this sheet of paper). To find in which of the two possible directions the field points, point the thumb of your right hand in the direction of the current; the fingers of your right hand will then curl in the direction of the field (here: toward the bottom of page).

2) To find the direction of the force on a straight wire carrying a current that is placed in an external magnetic field, point the fingers of the right hand in the direction of the flow of current; then curl your fingers into the magnetic field vector (as if you were “pushing” the vector representing the current direction into the magnetic field vector). Then, your right thumb will point in the direction of the force exerted on the wire carrying the test current. (Always curl your fingers through the smaller of the two possible angles – that is, through the angle that is between 0 and 180.)

We can now reinterpret the case of the two parallel wires carrying currents in the same (or opposite) direction. We can say, for instance, that the current on the left (I1) produces a magnetic field everywhere in space, and this field varies in magnitude depending on the distance from its source. The magnetic field B at a point a distance r from the wire carrying I1 is given by B = a I1  r, and so that is the magnetic field experienced by the wire on the right, which carries current I2. Now, the force F exerted on that wire on the right (assuming its length is “L”) is given by F = BI2L sin 90 = [a I1  r]  I2L  [1] = a I1 I2 L  r, which is exactly the same as the equation given on page 1 for the mutual force between two current-carrying wires. Note that the magnitude is the same whether the currents flow in the same or in opposite directions, because in both cases the angle  is 90.

We can also see that the directions given by this interpretation are consistent with what was described before. If we again take a top view of the two wires carrying current in the same direction (here, into the page), we can represent the magnetic field produced by the wire on the left with a set of vector arrows. Then, using the right-hand rule, we find that the direction of the force on the right-hand wire is toward the left, attracting it toward the other wire.

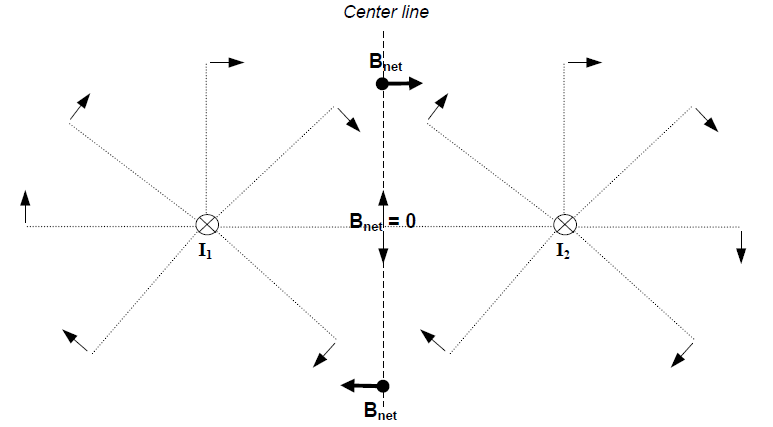
How does one find the net magnetic field when there are two or more source currents? The answer to this question has been found, by experiment, to be this: The net magnetic field is the vector sum of the individual magnetic fields produced by all the different source currents. (This is exactly what we found to be true regarding the net electric field, which is the vector sum of the contributions from each individual source charge). In the diagram below we have added a current I2, exactly equal to I1 in magnitude and also flowing into the page. Some of the magnetic field vectors produced by that second current are shown. At the point just between the two currents (at the middle of the dashed “center line”), the magnetic field contributions from I2 and I1 have the same magnitude but opposite directions and so the net field there is zero. Just above and below that point, the magnitudes are still equal (because the distances from I2 and I1 are the same along the center line) but only the vertical components of the two fields cancel each other. Therefore, the net field points along the horizontal direction.

What is the magnetic field pattern of a “current loop”? Of course, in order for a current to flow in a conducting wire the wire must be part of a complete circuit including a battery or other power source. The geometrically simplest circuit is simply a loop of wire (circular or square), connected to a battery. (Real wires do have some resistance to the flow of electric current, in contrast to the “ideal conductors” we have dealt with up to now.) Although most real “current loops” are not simple circles or squares, we can understand most of the properties of the real loops by closely examining those with simple shapes. Most of the important phenomena associated with magnetic forces and fields can be understood in the context of these simple current loops.
For instance, let’s start with a circular conducting loop connected to a battery:

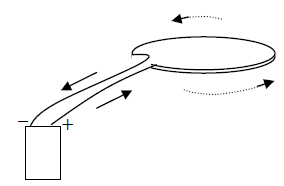
(This is a “perspective” view, and represents a circular loop with the plane of the loop out of the plane of the page. The arrows show the direction of flow of current.)

The two wires leading to the battery carry currents in opposite directions, and so the magnetic fields that they produce very nearly cancel each other out. For that reason, we will represent this type of current-loop circuit simply by showing the loop itself. We will also find that there are microscopic current loops in material objects, caused by the motions of electrons. These also may be represented by simple circular loops.
If we use the “right-hand rule” discussed above, we may find the magnetic field produced by such a current loop: if the current flows in the direction shown, the magnetic field inside the loop points upward, while just outside the loop it points downward:

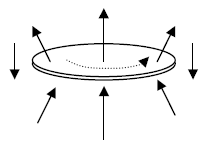
What is the connection between magnetic fields produced by electric currents, and the magnetic field of a “permanent” magnet made out of iron? The magnetic field pattern of the current loop is a good starting point for discussing the relationship between the magnetic field produced by currents flowing in wires, and the ordinary “permanent” magnets, made of iron and other materials, with which we are so familiar. What possible connection could there be between the two types of magnets: the one created by a current loop, and the one made of iron that has no obvious electric currents flowing in it?
The fact that there is, indeed, some connection is easy to show, although it was not recognized until 1820. (One reason for this is that it was difficult to produce large electric currents before that time.) We have already seen that a wire carrying a current will experience a force when in the presence of the magnetic field produced by another wire carrying a current. Will it experience a force in the presence of a permanent magnet as well? In fact, if we suspend a wire close to a strong permanent magnet and then allow a current to flow through that wire, we will see that a force is exerted on the wire. The wire will visibly move, and the direction of its movement will depend on its orientation with respect to the permanent magnet. So, if we use the term “magnetic field” to apply to the invisible entity (analogous to the electric field) that causes a force to be exerted on a current-carrying conductor, we have evidence that such a field is produced both by permanent magnets, and by other current-carrying conductors.
There are some other connections between the two types of magnets that could be considered very surprising. You may be familiar from everyday experience with the fact that compass needles are affected by the presence of magnets; the needles point toward or away from the ends, or “poles,” of the magnets. If we place a compass near a wire carrying a strong electric current, we will find that it is also affected by the wire. (This was the first groundbreaking experiment performed in 1820 by the Danish scientist Hans Oersted.) The compass needle will point in a specific direction, depending on precisely where it is located in the neighborhood of the wire. What is very remarkable is that the compass needle points in the direction of the magnetic field produced by the current in the wire, in a way that is consistent with our description of that magnetic field pattern (and with the diagram at the bottom of page two). So it seems that a compass needle may be used as an indicator of the direction of the magnetic field produced by electric currents.
If we now use a compass to examine the magnetic field pattern of a simple “permanent” magnet, such as a bar magnet, we find what first appears to be another remarkable coincidence: the magnetic field of the bar magnet is almost identical to the field pattern of the simple current loop.
Every permanent magnet has two distinct ends (here, the top and the bottom end); these ends are called “poles.” The term pole arises from the behavior of a compass needle, which is just a small bar magnet. The “north pole” is the term that has been applied to the end of the needle that will point toward the geographic north pole of the earth (i.e. in the arctic, north of Canada); the “south pole” is the other end of the magnet. We find that a compass needle will always point away from the north pole of a permanent magnet, and toward the south pole. According to our assumption that the compass needle points in the direction of the magnetic field at a given point, we conclude that the magnetic field points away from the north pole of the magnet and toward the south pole, as shown in the diagram. We may now also designate a “north pole” and a “south pole” for a current loop: the magnetic fields points away from the “north pole” side of the current loop (i.e., the “top side” as represented in the diagram at the bottom of page three.)

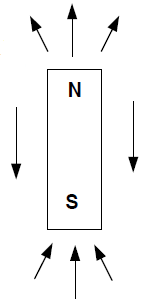
Question: Does the earth behave as if it had a north magnetic pole located above the arctic circle, or as if it had a south magnetic pole there? Answer: South magnetic pole located at the north geographic pole.
The bar magnet has almost the same magnetic field pattern as an object wrapped tightly with many loops of wire carrying a current. (Such an object is called a “solenoidal coil” or, for short, just a “solenoid.”) It is essentially just the magnetic field pattern of many individual current loops, added together. The natural question that arises is: Why should the magnetic field of the bar magnet resemble that of the current loop?
It is only within the past seventy years or so that the reason for this has been understood: in fact, there are electrical currents flowing around the edges of the bar magnet. However, these currents are microscopic in origin: they arise primarily from the motions of negatively charged electrons in the atoms of the material composing the magnet. The electrons are, of course, charged particles, and they behave just as if they were spinning around an axis similar to a globe spinning around its mounting axis. (The modern quantum mechanical picture of this process is more complicated, but this “spinning globe” model is often used to describe what is happening.) This spinning electron constitutes a tiny current loop, and there are many, many trillions of them in even a small piece of material. Each of these loops has its own magnetic field, pointed upward as shown in the diagram at the bottom of page three. It is just as if there were a huge number of very tiny magnets stuck inside the iron magnet.
In most materials, the orientations of these loops are completely random. The little “magnets” behave as if they were compass needles pointing every which way. But in some materials – principally, iron, cobalt, nickel and their alloys – these small current loops can be brought, at least temporarily, into the same orientation. In that way, all the small magnets point in the same direction. The net effect is the same as if the whole iron bar actually were wrapped with a solenoidal coil carrying an ordinary “macroscopic” [large-scale] electric current. And so, even in permanent magnets made out of chunks of iron, the source of the magnetic field ultimately is just an electric current, i.e. charged particles in motion. For this reason, the bar magnet and the simple circular current loop will behave in very similar ways when they are placed in an external magnetic field. (An external field is one created by sources outside of the magnet, or of the current loop.)

We can tie up many of the loose ends of this discussion if we study just how a current loop does behave when it is in the presence of an external magnetic field. We need to discuss two separate cases: (1) current loop in a uniform magnetic field; (2) current loop in a nonuniform magnetic field. Once we find out what will happen to the current loop in these situations, we should expect that the very same thing will hold true for a bar magnet – because, after all, the bar magnet really is just a current loop.
(1) Current loop in a uniform magnetic field. It is easiest to consider a square-shaped current loop, because we know how to find the forces exerted on straight lengths of wire placed in a magnetic field. We can examine the magnitude and direction of the force on each side of the square, and determine what will be the net effect on the loop.
Here we show two different situations. In each box, there is a uniform magnetic field and a current loop. The directions of the fields, and of the currents, are shown. By using the right-hand rule, we can determine the forces exerted on each side of the current loops; these forces are indicated by the dashed arrows and dot and cross symbols on each side. In two cases, the forces are zero (because the current flows either in the same direction as the current, or in the opposite direction).

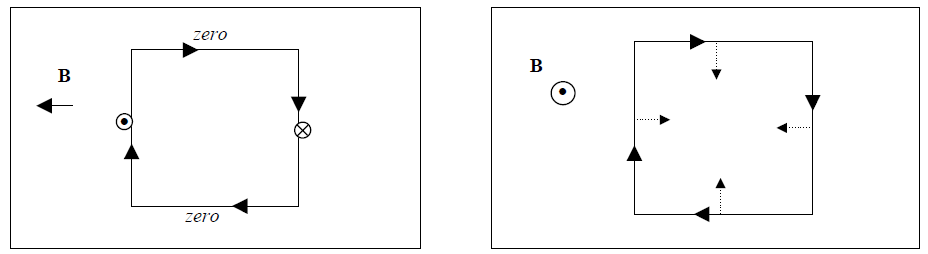
We find several important results:
(1) the net force on each loop is zero, because each force is matched by another with equal magnitude, and opposite direction.
(2) when the field is perpendicular to the plane of the loop (as it is in the right-side diagram), there will be no motion of the loop of any type even if it is completely free to move or rotate.
(3) When the field is parallel to the plane of the loop (as it is in the left-hand diagram), there will be a net torque on the loop, which will tend to make it twist or rotate. (In this case it would twist about a vertical axis drawn through the center of the loop.)
Now, we have only considered a very special case of a square loop with a particular direction of current flow, with two particular magnetic field orientations. However, those results are consistent with the following generalizations which can be shown to be true for all flat (planar) loops by more detailed mathematical calculations:
(1) A flat current loop of any shape, when placed in a uniform magnetic field, will experience no net force.
(2) A flat current loop of any shape, when placed in a uniform magnetic field where the magnetic field is perpendicular to the plane of the loop, will experience no net torque.
(3) A flat current loop of any shape, when placed in a uniform magnetic field where the magnetic field is not perpendicular to the plane of the loop, will experience a net torque.
As we pointed out above, we should expect these results to be applicable in some way to permanent magnets, because the permanent magnets are, in fact, really just current loops themselves. In fact, we do find the following to be true: (1) a bar magnet will experience no net force when placed in a uniform magnetic field; (2) a bar magnet, when placed in a uniform magnetic field, will experience a net torque unless it is aligned such that a line drawn from its south pole to its north pole is parallel to the direction of the magnetic field.
In both cases (the current loop and the bar magnet), the stable position is the one where an arrow drawn from the south pole to the north pole points in the same direction as the magnetic field. The opposite orientation is unstable; the slightest motion would cause the loop, or the magnet, to rotate around toward the stable orientation.
The diagram below should help to make all of this clear. It represents three identical current loops in a uniform magnetic field; we see the loops in a side view. The direction of current flow is represented for three of the sides of the loops (the other side is “hidden”). The forces on the top and bottom sides of the loop are shown; the forces on the other two sides of the loop are either zero (as in the case of the loop on the far left), or equal in magnitude, opposite in direction, and directed along the same line. Therefore, these (other side) forces cause neither a net force, nor a net torque. We can see, however, that that the forces on the top and bottom sides will result in a net torque unless the field is perpendicular to the plane of the loop (as it is for the loop on the far right). Similarly, the net effect on the bar magnets will match that of the current loops that have the same north pole-south pole orientation (i.e., no net torque on the bar magnet on the far right, but net torque on the other two.)

(2) Current loop in a nonuniform magnetic field. When a current loop is placed in a nonuniform magnetic field, the loop may experience a net force. This force will cause the loop to begin to move, if it was initially at rest before the field was present. It is these forces resulting from nonuniform magnetic fields that are responsible for the attractions and repulsions commonly observed with permanent magnets.
Here we show a side view of a current loop and a bar magnet; the magnetic field vectors point “outward” from the north pole of the bar magnet.

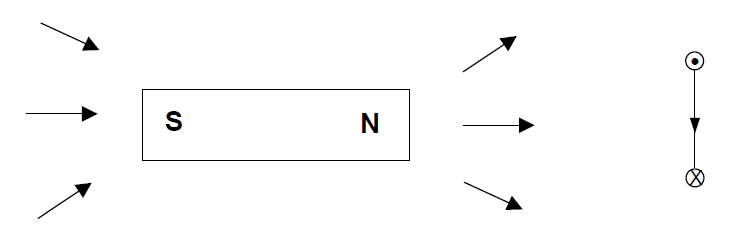
When we bring the current loop toward the bar magnet as shown in the diagram below, we see that the forces on the top and bottom sides of the current loop have a component directed toward the bar magnet. This is true of the other two sides of the loop as well, as is shown in the “head-on” view inside the dotted line. Here, the direction of the current is shown with small arrows, while the outward component of the magnetic field is indicated with larger arrows. The magnetic forces on each side of the loop (indicated with crosses) pull the loop toward the north pole of the bar magnet. [There is also a magnetic field component straight “out” of the page, but the forces on the loop resulting from this component of the field cancel each other out, as was shown for a similar case in the diagram at the bottom right of page 5.]

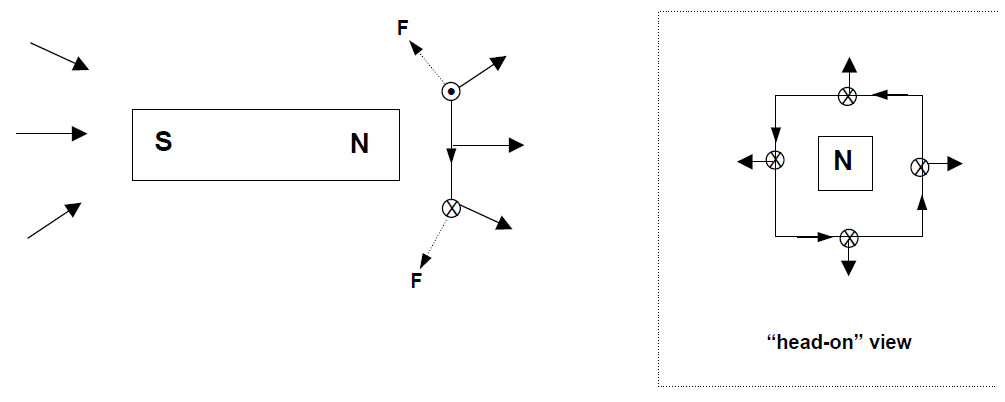
If we compare the diagram of the current loop shown here to those on the previous page, we can see that the “south pole” of the current loop is closest to the north pole of the bar magnet. If instead the “north pole” of the current loop were closer, the forces on the loop would reverse direction and the loop would have been repelled away from the bar magnet. This, of course, is exactly the behavior we observe when we bring two bar magnets together: like poles repel, and opposite poles attract.
The reason that the behavior is the same is because, as we mentioned before, the bar magnets actually are current loops – all of the many microscopic current loops add up to give the bar magnet the same properties as one large current loop. The reason that bar magnets are attracted to or repelled from each other is this: the magnetic forces on the current loops contained within the bar magnets result in net attractive or repulsive forces, depending on the relative orientation of two magnets. In the same way, two current loops near to each other would attract or repel each other, again depending on the relative orientation of the loops.
We can summarize all of these results with the following six separate cases, where the dashed arrows indicate the directions of the forces acting on the magnets and loops:

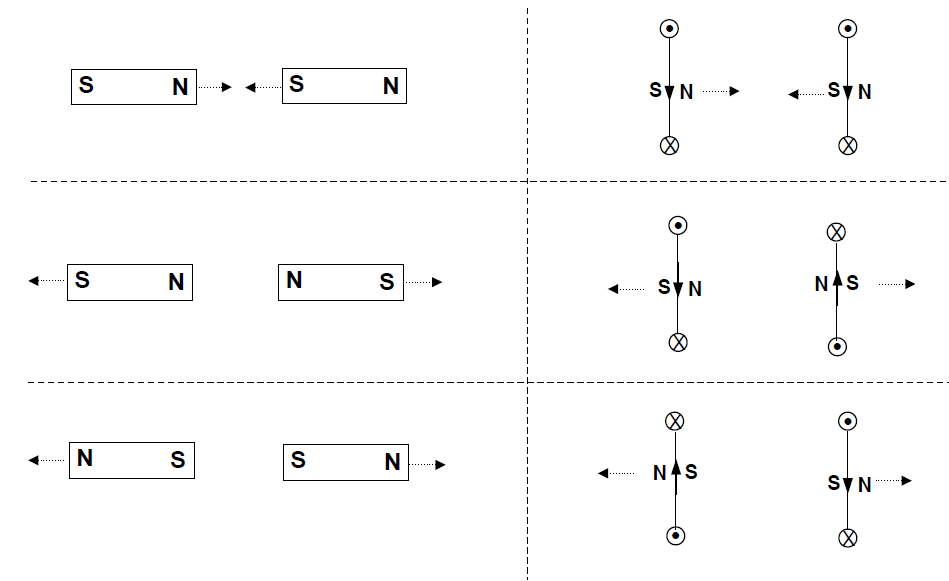
Now we can answer this question: why does a magnet attract an ordinary piece of metal that is not, itself, a magnet? The answer is that certain metals (such as iron), when they are in the presence of a magnetic field, become magnetized; that is, they are turned into magnets, at least temporarily. This is because the microscopic current loops within these materials can be brought into alignment by an external magnetic field, as is represented by the diagram . When this happens, the metal becomes a magnet with its own north and south poles, and it will experience magnetic forces (as shown in the diagrams on this page) just as would any other magnet.
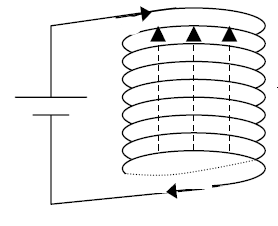
Suppose we want to create a uniform magnetic field, in which a current loop will experience no net force (but may experience a net torque)? One easy way to do this is to use a long cylindrical “solenoid,” or coil, which is essentially many small current loops piled up on top of each other. Inside of this cylindrical solenoid the magnetic field is very nearly uniform in magnitude and direction: it points along the long axis of the cylinder and its magnitude is proportional to the amount of current flowing within it, and to the number of loops (or “turns”) per unit length: $B\propto I{\frac {n}{L}}$

B  I n/L, where n is the number of “turns” and L is the length of the solenoid. (In this diagram, n = 8.)

Finally, we must mention the case of a single particle with charge q in the presence of a magnetic field. We know that a current will experience a force due to a magnetic field, and a current is just made up of individual charged particles which are on the move. Therefore it should not be a surprise to find out that a charged particle may experience a magnetic force if it is moving. The magnitude of the force is given by F = qvBsin$\theta$, where v is the speed of the particle and $\Theta$ is the angle between the direction of motion of the particle, and the direction of the magnetic field. From this equation, we can see that if the charge is moving in the same direction as the magnetic field – and so angle $\theta$
= 0 – there will be no force on the charged particle. This is consistent with what we found for a current-carrying wire: if the current is flowing in the same direction as the magnetic field, then it will not experience any magnetic force.