Electric Potential Energy

REVIEW OF CONCEPTS IN MECHANICS:

As we begin to examine the potential energy of charged particles, we will make use of several important concepts first brought up in the study of mechanical systems. First we start with definitions.
Definitions:
1. Kinetic Energy (KE) is the energy associated with the motion of an object; $KE={\frac {1}{2}}mv^{2}$
2. Potential Energy (U) is the energy associated with the position of an object;
3. Total Energy (TE) of an object is the sum of its kinetic and potential energies; $TE=KE+U$
4. Work (W) is a measure of the energy added to an object through the action of a force; $W=Fdcos\theta$
5. A Conservative Force is a force whose action does not alter an object’s total energy;
Defining Relationships:

In the equation for kinetic energy (KE), m is the mass of the object, and v is the speed of the object. In the equation for work (W), F is the magnitude of the force which is acting on some object, d is the magnitude of the displacement of the object while it is being acted on by that force, and $\theta$ is the angle between the direction of the force, and the direction of the displacement. (Magnitude of displacement d is equal to the distance the object moves, if it moves in a straight line.) ‘’This equation for work assumes that the force is constant, and it may not be used in situations where the force changes in magnitude or direction while the object is moving.’’

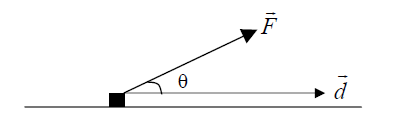
Figure shows a small box being pulled across a frictionless surface by a force F, such as might be supplied by a handle on a suitcase.
Everything above consists of definitions. The fundamental physical principles themselves can be summarized in only two equations:
$\Delta KE=W_{net}$ i.e. the work-kinetic energy theorem. Note "net" implies work done by both conservative and non-conservative forces

$\Delta TE=W_{nonconservative}$ a more useful description where the work done by conservative forces is described as potential energy

Here, $\Delta KE$ is the change in kinetic energy, which is equal to: $\Delta KE=KE_{final}-KE_{initial}$
similarly,
$\Delta TE$= change in total energy, and we have this important relationship:
$\Delta TE=\Delta KE+\Delta U$)
We can rewrite this last one in a more familiar form:
$TE_{final}=TE_{initial}$
$KE_{f}+U_{f}=KE_{i}+U_{i}$
This is a statement of conservation of energy under the special case of no external forces to the system [no non-conservative forces].
The “Work-Energy” theorem says that the change in the kinetic energy of an object is equal to the net work done on that object. So, for instance, if positive work is done, the object will speed up. (Note: The change in KE is actually equal to the net work done on the object, i.e., the work done by the ‘’net force’’.)
The Conservation of Energy equation says that any change in total energy of an object is equal to work done only by nonconservative forces on that object. This implies that if only conservative forces are acting on the object, its total energy does not change.

The Electric Force is Conservative

The forces we have been concerned with fall into two categories:

Conservative Forces:	Nonconservative Forces:
Gravitational Force Elastic force of an ideal spring Electrical Force	friction push or pull due to direct contact with another object or a person

Here, we will only be concerned with the electrical force, and a push or pull due to direct contact
with another object or person.

---

Question #1: If only the electrical force is acting on an object – no friction, nor push or pull by direct contact – what will happen to the sum of the object’s kinetic and potential energies:

1. increase,
2. decrease,
3. remain the same, or
4. may increase or decrease, depending on the situation.

Answer: C. Explain why.

---

We can now summarize the two general principles that will guide us in understanding electric potential energy:

1. If a charged particle is being acted on only by electrical forces (no push or pull by direct contact), then ‘’the total energy of the charged particle must remain constant.’’ This means that $\Delta TE=0$ , and so $\Delta U+\Delta KE=0$ Therefore, an increase in U equals a decrease in KE (and vice-versa): $\Delta U=-\Delta KE=0$
   
2. If a charged particle is being acted on by both electrical forces and direct-contact [nonconservative] forces, then the change in the total energy of the charged particle is equal to the net work done by the nonconservative forces: $\Delta TE=W_{nonconservative}$
   

We will consider two basic physical situations:

1. a region where the electric field is uniform (same magnitude and direction everywhere);
   
2. a region in the neighborhood of a single, isolated “source” charge. Most real situations are more complicated than these, but we can understand most of the basic ideas by looking at these two situations.
   

I. Region where electric field is uniform (i.e., electric field has same magnitude and direction everywhere in region)

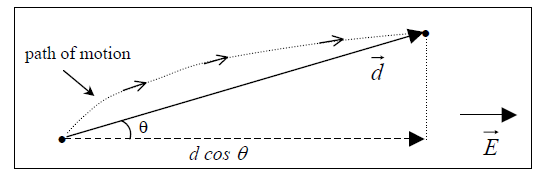
Let’s consider what happens to a positive test charge +q when we release it from rest in this region. Its initial kinetic energy is zero, but as time goes on, the particle sUeds up (due to the electrical force acting on it) and so it gains kinetic energy. Since only the electrical force is acting on it (we assume), its total energy must be constant. Therefore, its potential energy must be decreasing. How much will its potential energy change if it travels a distance d? The decrease in potential energy must be equal to the increase in kinetic energy, and – according to the Work-Energy theorem – this is equal to the work done on the particle by the electric force. If the particle is released from rest, it will travel in the direction of the electric field (since that’s the direction of the force acting on it). The magnitude of the force acting on it is equal to qE¸ so we have the following relationship:
$-\Delta U=\Delta KE=W=Fdcos\theta =Fdcos0=Fd=qEd$
What this equation says is this: If a positive charge q travels a distance d in the direction of a uniform electric field with magnitude E, then the potential energy of this charge will decrease by an amount equal to qEd. (We can see that its potential energy decreases, because if qEd is positive, then $\Delta U$will be negative:
$\Delta U=-qdE$).
That means that the final value of the potential energy is less than the initial value, by an amount equal to qEd.
(If the charge does not travel in a straight line, then the change in potential energy is given by qEd where d is the magnitude of the charge’s displacement.)

Now, where is the potential energy, U, equal to zero? The answer is, we can set it equal to zero anywhere we want. This is because the quantity that really has meaning is $\Delta U$– the change in U – not the absolute value of U itself. However, we usually choose some convenient location at which to set U = 0. Then, we will often speak of the “U” value of the charge at some point, even though what we really mean is the difference in U values between that point, and the point where we have set U equal to zero.

---

Question #2: Suppose a charged particle, which was released from rest, loses 3 J of potential energy while traveling a distance of 4 m in a uniform electric field. (a) How much potential energy will it lose if it travels a distance of 12 m in this same field? (b) How much kinetic energy will it gain if it travels a distance of 10 m in this same field? Answers: 9 J; 7.5 J

II. Region in neighborhood of a single, isolated “source” charge Q

The situation in this case is more complicated, because the electric field is not uniform in the neighborhood of an isolated source charge. The electric field at any point in that neighborhood points away from a positive source charge (and toward a negative source charge). Thus, the direction that the field points depends on where you are located. Also, the field has larger magnitude near the source charge (remember that the magnitude is given by E = k|Q|/r2).
Now, suppose we have a positive source charge Q fixed in position at the origin, and we place a positive test charge q somewhere in the neighborhood, initially at rest, at a distance from the source charge Q. What will happen to the test charge when it is allowed to move freely? It will begin to move away from the source charge (since it’s repelled), and as it moves, it will speed up. (Since it always experiences a force the force will cause it to accelerate, and so its speed continues to increase). Since its kinetic energy must be increasing, once again we see that its potential energy must be decreasing (because, again, its total energy must remain constant). This tells us that the farther away it gets from the source charge, the smaller will be its potential energy.
How much will the potential energy change? Again, because TE = constant, we will have:
$\Delta U=-\Delta KE=-W$

But in this case, we cannot use because the force is not constant. Using the methods of calculus it is possible to find the work done on the charge by the electric force when the charge changes its position.
$W=\int _{ri}^{rf}F\cdot dx=\int _{ri}^{rf}qE\cdot dx=\int _{ri}^{rf}q{\frac {kQ}{r^{2}}}\cdot dr=-q{\frac {kQ}{rf}}+q{\frac {kQ}{ri}}$

This leads to the following result:
$\Delta U=U_{final}-U_{initial}=-W={\frac {kQq}{r_{final}}}-{\frac {kQq}{r_{initial}}}$

From this we see, as we expect, that as the charge q moves away from Q its potential energy decreases. (Since $\Delta U$will be negative, which means that U is decreasing.) Does its U ever get down to zero? In a case like this, we usually decide to set the value of U equal to zero when the test charge is infinitely far away from the source charge; this is when the value of r is infinity. (This choice usually makes problems of this type easier to solve.) Given this choice, the potential energy U of a test charge q a distance r from a source charge Q will be given by the following simple equation:

$U(q)={\frac {kQq}{r}}$
Note that for a given source charge Q and a given test charge q, the potential energy of the charge q depends only on its position. It does not matter how charge q arrived at that position or what path it followed.
Now, what if the test charge is negative, i.e., q < 0 (while the source charge Q remains positive)? That equation seems to say that the potential energy of a negative test charge would be negative; does that make sense? Well, suppose we place a negative test charge at rest in the neighborhood of Q; what will happen? It will start to move in toward Q (since it’s attracted); so its kinetic energy increases as r gets smaller. Or, to put it another way, its U increases as r increases. But we have set U = 0 when $r=\infty$  ; how could U be increasing up to a value of zero? Answer: By starting out at some negative value. Therefore, the equation is actually correct for q < 0.

Now, what about for a negative source charge (Q < 0)? You should be able to devise an argument to show that the same equation above works in that case as well.

Examples

1. Two parallel metal plates are connected to a battery, which creates a uniform electric field between the plates. The electric field points from the left-side plate to the right-side plate. A 2-C charge is held at rest somewhere between the plates, and then released. When it strikes the right-side plate, its kinetic energy is 6 J, and its potential energy is 0 J. What was its potential energy just before it was released?
   
2. A uniform electric field of magnitude 4 N/C is set up in a region 8 m wide. A 2-C charge is held at rest on a wall on one side of the region, and then released. What is its kinetic energy when it strikes the wall on the other side?
   
3. A 3-C charge is fixed at the origin. A 2-C charge is held 3 m from the origin, and then released. Later, a 1-C charge is held 2 m from the origin, and it is released. All three charged particles have the same mass. Which of these statements is true, in comparing the 2-C and the 1-C charges:
   

1. The 2-C charge will eventually attain the fastest speed (i.e., when it is very far from the origin.)
2. The 1-C charge will eventually attain the fastest speed (i.e., when it is very far from the origin.)
3. Both the 1-C and the 2-C charges will eventually attain the same speed.

1. An object with a mass of 2 kg and a net charge of 4 microC is shot from a gun aimed at the origin. The gun is located 20 km from the origin; the initial speed of the object is 3 m/s. A particle with a charge of 0.001 C is fixed at the origin. How close will the object get to the origin before it slows to a stop and starts back the other way?
   

---

Answers and Explanations:

1. When it strikes the right side plate, the total energy (TE) of the charge is 6 J (6 J + 0 J). Since its total energy does not change, that must have been the original value of its total energy as well. Initially, it was at rest so its kinetic energy was zero. Therefore, the initial value of its potential energy must have been 6 J.
   
2. The change in the kinetic energy is equal to the work done on the charge. The charge is released from rest, and so will travel in the same direction as the electric field. Therefore, we get This tells us that the change in the kinetic energy was 64 J. Since the initial value of the KE was 0 J, we see that the final value of the KE, when the charge strikes the wall, is 64 J.
3. To figure out which charge eventually attains the fastest speed, we have to remember that the total energy of each charge will not vary as it moves, since only electrical forces are acting. For each charge, the initial kinetic energy is zero, since they are released from rest. Therefore, all of their energy is initially potential energy. Eventually, they will move very far away from the origin due to the repulsive force. In fact, they will eventually move so far that their potential energy is very close to zero. (Remember that their potential energy is given by U = kQq/r. When r is very large, U is very small.) So, when they get very far from the origin, their potential energy is nearly zero and nearly all of their total energy will be kinetic energy. Eventually, their kinetic energy will be nearly equal to the amount of potential energy that they had at the moment they were released. Since they both have the same mass, whichever has the largest final kinetic energy will also have the fastest final speed.
   So, all we have to do is figure out which one has the largest initial potential energy. The initial potential energy of the 2-C charge is given by by U = k(3)(2)  (3) = 2k J. The initial potential energy of the 1-C charge is given by U = k(3)(1)  (2) = 1.5k J. Therefore, the 2-C charge has the larger initial potential energy. So, it will eventually have the largest kinetic energy, and therefore the fastest speed. (So answer is “A.”)
   
4. The initial total energy equals the final total energy: KE(initial) + U(initial) = KE(final) + U(final). We know that KE(initial) = ½ mv2 = (0.5)(2)(9) = 9 J, and KE(final) = 0 J. U(initial) is nearly zero, since U = kQq/r and r(initial) = 2  104 m. Then we have TE(initial) = TE(final)  9 J + 0 J = 0 J + U(final), so U(final) = 9 J. Then kQq/r = 9 J, or r = kQq  9 J = (9  109 )(0.001)(4  10–6 )  9 = 4 m.