Electric Potential

Chapter 4 Notes: Electric Potential

What is the difference between electric potential energy and electric “potential”?

We have seen that a charged particle may have different values of electric potential energy, depending on its location. As it accelerates under the influence of the electric field the charge’s kinetic energy increases, and so its potential energy must be decreasing (since its total energy remains constant). So, when it is released from rest, a test charge moves toward a location where its potential energy is lower. If we specify a reference point where the potential energy is zero, we may “map out” the potential energy value of the test charge at every possible location.
An example is a test charge q1 in the neighborhood of an isolated source charge Q. If q1 is a distance r from Q its potential energy is k q1Q/r, as described in the Chapter 3 Notes.
Suppose we draw a circle of radius ra around Q, and suppose q1 is located somewhere on that circle. What would happen to the potential energy of q1 as it moves ‘’around’’ that circle? Answer: Its PE will remain constant. Let’s suppose that the PE of q1 at a point anywhere on this circle is equal to 20 J.

Now suppose we draw another circle, this one at a radius rb = 2ra, and we put charge q1 on ‘’that’’ circle. Would its PE be greater than, less than, or the same as it was on the smaller circle? Answer: Less than. [PE(rb) = ½ PE(ra) = 10 J.]

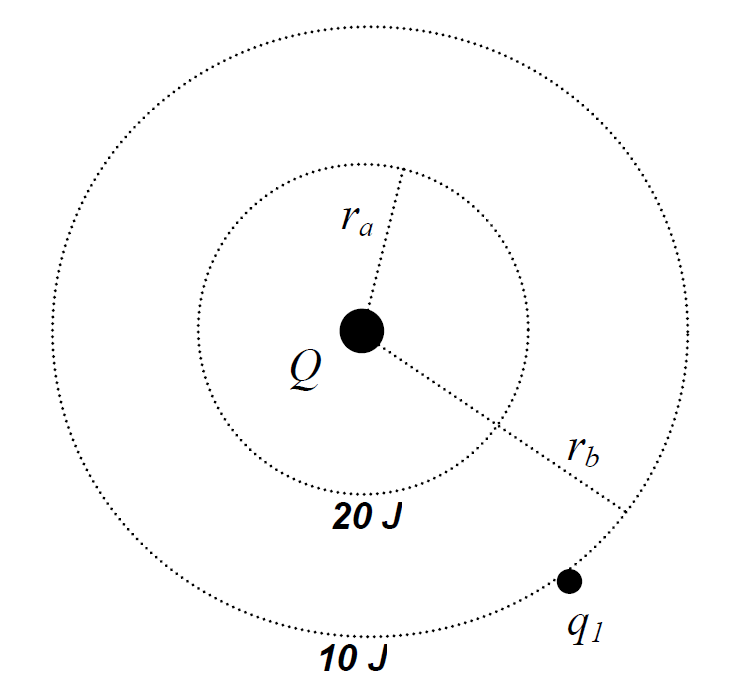
We are beginning to “map out” the potential energy of test charge q1 at various points in the neighborhood of source charge Q. We can see that this map will consist of a set of circles of different radii; at any point on a given circle, the PE of q1 will have one specific value. As q1 moves out to larger circles, its PE decreases. We could refer to various locations on this map as “the 20 J circle,” “the 10 J circle,” “between the 20 J circle and the 10 J circle,” and so on.
However, there is a drawback to this map: the numerical values depend on ‘’which’’ test charge we use! Suppose we put a charge q2 = 4q1 on the “20 J” circle. Would its PE be greater than, less than, or equal to 20 J? Answer: Greater than. [PE(q2) =4PE(q1) = 80 J.] Our map would be more useful if it were completely independent of which test charge we used.
‘’For this reason, we will define a new quantity called electric “potential” [symbol: V] (not the same as “potential energy”); a map (or diagram) of “potential” will allow us to determine the potential energy of any test charge at any point in the region.’’
Electric Potential V is defined as “potential energy per charge,” or as the ratio:
$V={\frac {PE(q)}{q}}$

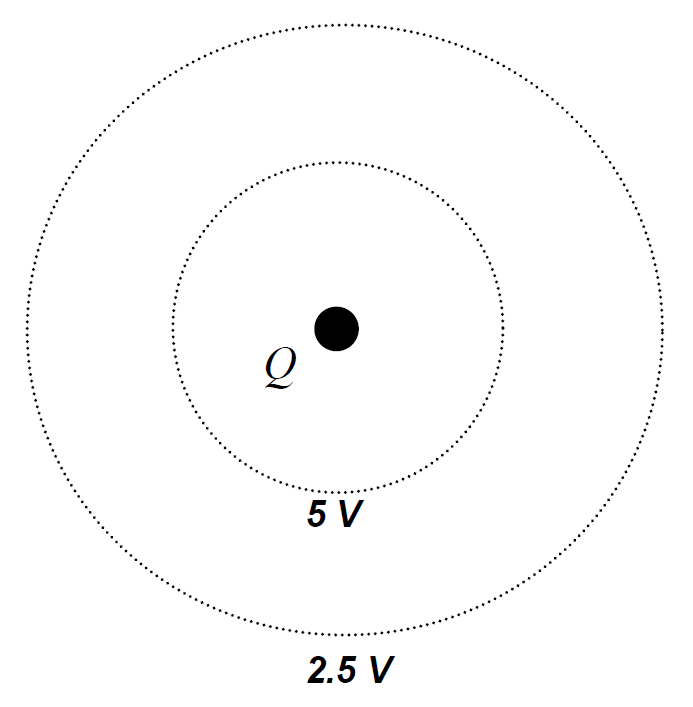
In our example, the inner circle was a “20 J” circle for charge q1, and an “80 J” circle for charge q2. (This was because PE = k qQ/r , and q2 = 4q1.) Let’s suppose that charge q1 = 4 C, and charge q2 = 16 C. If we now calculate the ‘’potential ‘’V on the inner circle using q1, we get V = 20 J  4 C = 5 J/C; using q2, we get V = 80 J  16 C = 5 J/C. So we get V = 5 J/C no matter ‘’which’’ test charge we use. The unit of potential is called the ‘’volt’’ (V) [1 V = 1 J/C] and so we may now identify the inner circle as the “5 V” potential circle, and the outer circle as the “2.5 V” potential circle:

There are two very useful relationships (really just one relationship, written two different ways) that follow directly from the definition of the potential. They relate the “potential difference” ($\Delta V_{AB}=V_{B}-V_{A}$ )

$\Delta V_{AB}={\frac {\Delta PE(q)_{A\rightarrow B}}{q}}$

$=\Delta PE(q)_{A\rightarrow B}=q\Delta V_{AB}$

between two points A and B, to the ‘’change in potential energy’’ of a charge q as it moves from point A to point B ($=\Delta PE(q)_{A\rightarrow B}$ ):
We can now answer a question such as this: If a 3-C charge moves from the 5-V circle to the 2.5-V circle, what will happen to its kinetic energy?
Answer: Its PE will decrease by an amount equal to qV = (3C)(–2.5V) = 7.5 J; therefore, its KE must ‘’increase’’ by +7.5 J.
The word “voltage” is often used as shorthand for “potential difference” (V) . When you hear “voltage,” you should always think of the ‘’difference’’ in electric potential between two different points. We often loosely use the term “potential difference” to refer to the ‘’absolute value’’ of potential difference, or V .

We can now map out a region where an electric field is present by representing electric potential, instead of (or in addition to) drawing vectors to indicate the electric field at various points. This is normally done by drawing a whole set of lines called “equipotential lines.” An “equipotential line” is a line along which the electric potential does not change. Our circles in the diagrams above are equipotential lines, since the potential has a constant value along any given circle. If a charged particle moves along an equipotential line, its potential energy is not changing.
We can look at a “potential diagram” and immediately determine certain features about the ‘’magnitude ‘’and ‘’direction’’ of the electric field that is present in the region. For instance: Consider the electric field vectors in the region between two equipotential circles.
Will they point toward the higher-potential circle, toward the lower-potential circle, or in a direction tangent to both circles? Answer: They will point from the higher-potential circle toward the lower-potential circle.
‘’Explain how you can determine this by considering the motion of a test charge.’’

We can also see here an example of a general relationship:
‘’The electric field vector at a point in space always points perpendicular to the equipotential line that passes through that point.’’
It is also possible to determine the ‘’magnitude’’ of the electric field at various points on a potential diagram. There are two relationships that will help us do this:
1) ‘’In a region where the electric potential is constant (uniform), the electric field is zero.’’ Suppose a charge is drifting in a region where the electric potential has the same value everywhere. That means that the charge has the same value of potential energy at every point, and so its kinetic energy can not be changing, either. Therefore, the charge’s velocity is constant and unchanging as well. We must conclude that no force is acting on this charge to accelerate it, and so ‘’the electric field must be zero in this region.’’ By a similar argument, we can see that if the electric field is zero in some region, the electric potential must have a uniform, unchanging value throughout that region.

‘’When comparing two regions of equal size, the region with the largest variation of electric potential will have the electric field with the largest magnitude.’’ Here’s an example: Let’s consider two regions of the same size, each of which has a uniform electric field present. Suppose we put a +3C charge at point P in region A, and let it move freely. We know that the electric field points from ‘’higher’’ potential to ‘’lower’’ potential, and so the charge will accelerate to the right. When it approaches the right side, its kinetic energy will have increased by an amount equal to its potential energy loss, so KE = –PE = –qV = (3C)(–3V) = 9 J. If we do the same thing in region B, we can see that when the charge has covered about the same amount of distance as before, its kinetic energy will now have increased by –(3C)(–5V) = 15 J. Since KE = W, more work was done by the electric force in region B. Since in this situation W = Fd and d is the same in both cases, the force F must be greater in region B. Since E = F/q and we used the same q in both regions, the electric field magnitude E must be greater in region B. Qualitatively, we can associate more “tightly packed” equipotential lines (as in region B) with larger-magnitude electric fields. In the case of a uniform electric field (as in A and B), there is a simple relationship: E = V/d.

2)
There are a two other important facts related to electric potential:
i) ‘’Every point in a single piece of conducting material ‘’has the same value of electric potential. We say that the conductor is an “equipotential volume.” A ‘’conductor’’ is a material in which electric charges can move freely from place to place. (Actually, it is the negative charges – the electrons – which move, while the positive charges stay fixed. However, we will usually speak ‘’as if’’ it is the positive charges that are really moving. This is a conventional choice, which helps to simplify the discussion.) In an “ideal” conductor, there is no electric field present. The charges always arrange themselves in such a way that the net electric field in the conductor is zero. According to #1 above, this means that the value of the potential does not change anywhere inside the conductor. Any piece of conducting material – such as a wire – in direct contact with another piece of conducting material – such as a piece of metal – will form one ‘’single’’ conducting volume, which will all be at the same electric potential.

ii) A ‘’ battery’’ is an electrochemical device the supplies electrical energy, and has two “ends” which are called the positive and negative “terminals.” The symbol for a battery consists of two parallel lines, in which the longer line corresponds to the positive terminal. The battery uses chemical reactions to ensure that the ‘’positive’’ terminal is at a ‘’higher’’ electric potential than the negative terminal. Moreover – and this is very important – in an ideal battery, the ‘’potential difference between the terminals always has the same value’’.

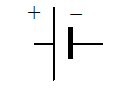
CAPACITANCE: A “capacitor” is a device that is used to store electrical charge and electrical energy. (When it stores charge, it also stores energy.) It is very different from a battery, because it can be “emptied” of all of its charge and energy in a very short time period – usually less than one second. We say that the capacitor is “discharged” when it loses its charge, and that it becomes “charged” when it acquires its charge and its energy. Capacitors of different types are used in thousands of applications, including cardiac defibrillators, electric circuits for radios, electronic flash lamps, computer memory chips, and nearly all electronic devices.

Capacitors come in many varieties of shapes and sizes, but fundamentally they all consist of one thing: a single pair of conducting objects, fixed in positions close to each other (but not touching). Usually, the two conducting objects are identical to each other, and often they are shaped like plates or sheets. (Sometimes the sheets are flexible and are rolled up to form a compact cylinder.) Perhaps the simplest form of capacitor is a single pair of parallel metal plates, where the distance between the plates is relatively small compared to the size of the plate. If we want to “charge” this capacitor, we might connect it to a battery (one plate to the positive terminal, the other plate to the negative terminal). Then one plate becomes positively charged, with charge +Q, while the other plate acquires negative charge –Q. This particular arrangement is very useful, because it can be shown that the electric field in the region between the plates is very nearly uniform. In fact, we will always assume that the field between the plates is completely uniform. As we have seen, in this case the equipotential lines form a set of equally-spaced parallel lines.

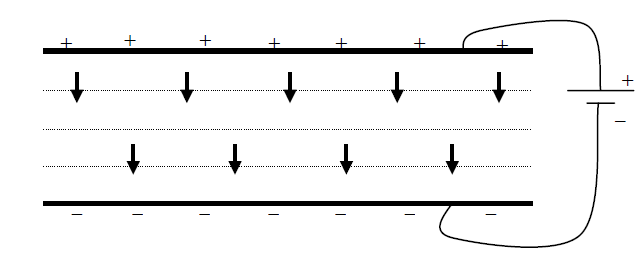
The quantity of charge that is stored on the plates depends on the potential difference $\Delta V$ between the positive plate (which is at higher potential) and the negative plate ($\Delta V$ = V+ – V– ). A larger $\Delta V$ leads to a larger Q. In fact, these quantities are proportional to each other: Q = C $\Delta V$ , where C is a proportionality constant. (Why is this? A large amount of charge on the plates implies that the electric field between the plates will have a large magnitude – and so a charged particle moving from one plate to the other will undergo a large change in kinetic (and potential) energy. This means that the potential difference V would also be large.) The proportionality constant C is called the “capacitance” of the capacitor, and it depends only on the size, shape, and spacing of the conducting plates. It will be the same for any value of Q or $\Delta V$ . (The unit of capacitance is called the farad [symbol: F] so 1 F = 1 C/V.) The amount of energy that is stored by the capacitor depends both on the capacitance, and on the potential difference: Energy stored = ½ C ($\Delta V$ )2. (This is the energy provided by the capacitor when it discharges)
Examples:
1. A 27-C charge is fixed at the origin. When a 3-C charge is placed at point P, it has a potential energy of 9 J. If the 3-C charge is now removed, what will be the electric potential experienced by a 6-C charge placed at point P? Answer: V = PE/q, so V = 9 J  3 C = 3 V. This will be the potential experienced by any charge at point P.
2. How much external work must be done to force a +3-C charge to move from the negative plate to the positive plate of a parallel plate capacitor that is connected to a 6-V battery? (Assume that the speed of the charge does not change.) Answer: $W_{nonconservative}=\Delta TE+\Delta PE=0J+\Delta PE=q$ = (3 C)(6 V) = 18 J.
3. Several equipotential lines are shown, with potential values indicated. Where should you place a proton so that it would experience the largest magnitude of electrical force?
Answer: Point A; this is where the equipotential lines are most “densely” packed, and where V/x (which is approximately equal to E) is the greatest.

4. A capacitor is connected to a 5-V battery, which results in a net charge of +3 C on the positive plate. Suppose the capacitor is disconnected from the 5-V battery, and connected instead to a 10-V battery. What will be the charge on the negative plate?
Answer: Q = C V; here, C does not change, but V is doubled. Therefore, the charge on the positive plate will now be equal to +6 C, while that on the negative plate will be –6 C.