Magnetic Fields: Difference between revisions
No edit summary |
No edit summary |
||
| (17 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
*[https://openstax.org/books/university-physics-volume-2/pages/11-introduction University Physics Volume 2: Chapter 11 - Magnetic Fields] | *[https://openstax.org/books/university-physics-volume-2/pages/11-introduction University Physics Volume 2: Chapter 11 - Magnetic Fields] | ||
== Ferromagnets and Electromagnets | = Introduction = | ||
<youtube>Aq82Zsr4dvI</youtube> | |||
= Ferromagnets and Electromagnets = | |||
<youtube>8ixOzpLNlMY</youtube> | <youtube>8ixOzpLNlMY</youtube> | ||
| Line 24: | Line 27: | ||
= Magnetic Field Lines = | = Magnetic Field Lines = | ||
Magnetic field lines represent the direction and strength of the magnetic field. | <youtube>IJgzVaTPEow</youtube> | ||
<youtube>NWUgK8W-4JM</youtube> | |||
Magnetic field lines represent the direction and strength of the magnetic field. Magnetic field lines go from the north pole to the south pole of a magnet (the direction a compass would point). The form loops and never cross. | |||
= Motion of a Charged Particle in a Magnetic Field = | = Motion of a Charged Particle in a Magnetic Field = | ||
== Force on a Moving Charge == | == Force on a Moving Charge == | ||
[[File:RHR-lorentz.png|thumb|right|400px|Lorentz-Force Right-Hand-Rule for positive charges based on Cross-Product Right-Hand-Rule]] | |||
The force <math>\vec{F}</math> on a moving charge <math>q</math> in a magnetic field <math>\vec{B}</math> is given by the Lorentz force: | The force <math>\vec{F}</math> on a moving charge <math>q</math> in a magnetic field <math>\vec{B}</math> is given by the Lorentz force: | ||
* Formula: <math>\vec{F} = q \cdot (\vec{v} \times \vec{B})</math> | * Formula: <math>\vec{F} = q \cdot (\vec{v} \times \vec{B})</math> | ||
| Line 35: | Line 42: | ||
* <math>\vec{v}</math> is the velocity of the charge, | * <math>\vec{v}</math> is the velocity of the charge, | ||
* <math>\times</math> denotes the cross product. | * <math>\times</math> denotes the cross product. | ||
<div style="clear:both;"></div> | |||
<youtube>dFT7-_s0jh0</youtube> | |||
<youtube>7MBawzone30</youtube> | |||
<youtube>orsMYomjwIw</youtube> | |||
== Applications == | == Applications == | ||
| Line 45: | Line 57: | ||
=== Mass Spectrometer === | === Mass Spectrometer === | ||
Used to measure the mass-to-charge ratio of ions | <youtube>J-wao0O0_qM</youtube> | ||
Used to measure the mass-to-charge ratio of ions. | |||
=== Cyclotron === | === Cyclotron === | ||
<youtube>HmVGGs6Dxp8</youtube> | |||
A type of particle accelerator that uses a perpendicular magnetic field to accelerate charged particles in a circular path. | A type of particle accelerator that uses a perpendicular magnetic field to accelerate charged particles in a circular path. | ||
= | = Combined Fields = | ||
== Force on a Moving Charge due to Electric and Magnetic Fields == | == Force on a Moving Charge due to Electric and Magnetic Fields == | ||
| Line 66: | Line 74: | ||
== Thomson Experiment (Discovery of the Electron) == | == Thomson Experiment (Discovery of the Electron) == | ||
Used crossed electric and magnetic fields to determine the charge-to-mass ratio of the electron. | Used crossed electric and magnetic fields to determine the charge-to-mass ratio of the electron. | ||
<youtube>Rb6MguN0Uj4</youtube> | |||
== Hall Effect == | == Hall Effect == | ||
The creation of a voltage difference across an electrical conductor, transverse to the electric current and the applied magnetic field. | The creation of a voltage difference across an electrical conductor, transverse to the electric current and the applied magnetic field. | ||
<youtube>wpAA3qeOYiI</youtube> | |||
= Magnetic Force on a Current-Carrying Wire = | = Magnetic Force on a Current-Carrying Wire = | ||
[[File:RHR-wire.png|thumb|right|400px|Direction of the force on a wire RHR based on Cross-Product RHR]] | |||
The force on a wire of length <math>L</math> carrying current <math>I</math> in a magnetic field <math>B</math> is: | The force on a wire of length <math>L</math> carrying current <math>I</math> in a magnetic field <math>B</math> is: | ||
* Formula: <math>\vec{F} = I \cdot (\vec{L} \times \vec{B})</math> | * Formula: <math>\vec{F} = I \cdot (\vec{L} \times \vec{B})</math> | ||
<youtube>GSIPBaaAYKc</youtube> | |||
<div style="clear:both;"></div> | |||
= Torque on a Current Loop - the Electric Motor = | = Torque on a Current Loop - the Electric Motor = | ||
A current loop in a magnetic field experiences torque, which is the basis for electric motors. | A current loop in a magnetic field experiences torque, which is the basis for electric motors. | ||
* Formula: <math>\tau = n \cdot I \cdot A \cdot B \cdot \sin(\theta)</math> | * Formula: <math>\tau = n \cdot I \cdot A \cdot B \cdot \sin(\theta)</math> | ||
| Line 86: | Line 104: | ||
< | == Magnetic Dipole == | ||
A magnetic dipole consists of a closed loop of electric current or a pair of opposite magnetic poles separated by a distance. The magnetic moment <math>\vec{\mu}</math> is a vector quantity that points perpendicular to the plane of the current loop and is proportional to the current and the area of the loop: | |||
* Formula: <math>\vec{\mu} = N \cdot I \cdot A \cdot \hat{n}</math> | |||
Where: | |||
* <math>\vec{\mu}</math> is the magnetic dipole moment, | |||
* <math>N</math> is number of turns, | |||
* <math>I</math> is the current, | |||
* <math>A</math> is the area of the loop, | |||
* <math>\hat{n}</math> is a unit vector perpendicular to the loop, following the right-hand rule. | |||
**Right-hand rule**: Curl the fingers of your right hand in the direction of the current around the loop. Your thumb will point in the direction of the magnetic dipole moment <math>\vec{\mu}</math>. | |||
== Torque on a Magnetic Dipole in a Magnetic Field == | |||
[[File:RHR-dipole.png|thumb|right|400px|Direction of the torque on a dipole RHR based on Cross-Product RHR]] | |||
When a magnetic dipole is placed in an external magnetic field <math>\vec{B}</math>, it experiences a torque <math>\vec{\tau}</math>, which tends to align the dipole with the field: | |||
* Formula: <math>\vec{\tau} = \vec{\mu} \times \vec{B}</math> | |||
Where: | |||
* <math>\vec{\tau}</math> is the torque, | |||
* <math>\vec{\mu}</math> is the magnetic dipole moment, | |||
* <math>\vec{B}</math> is the magnetic field. | |||
== Potential Energy of a Magnetic Dipole == | |||
The potential energy <math>U</math> of a magnetic dipole in a magnetic field is given by: | |||
* Formula: <math>U = -\vec{\mu} \cdot \vec{B}</math> | |||
Where: | |||
* <math>U</math> is the potential energy, | |||
* <math>\vec{\mu}</math> is the magnetic dipole moment, | |||
* <math>\vec{B}</math> is the magnetic field. | |||
The potential energy is minimized when the dipole is aligned with the magnetic field, and maximized when it is opposite to the magnetic field. | |||
<youtube>_saTdQ9AEnM</youtube> | |||
<youtube>Xi7o8cMPI0E</youtube> | |||
= Simulations = | = Simulations = | ||
| Line 103: | Line 154: | ||
<!--* [http://www.phy.syr.edu/courses/java-suite/crosspro.html Cross product of two vectors-with expalnations]--> | <!--* [http://www.phy.syr.edu/courses/java-suite/crosspro.html Cross product of two vectors-with expalnations]--> | ||
<br class="clear"/> | |||
Back to [[Electricity_and_Magnetism]] | Back to [[Electricity_and_Magnetism]] | ||
<br class="clear"/> | |||
Next: [[Sources of Magnetic Fields - Biot Savart]] | |||
Latest revision as of 15:52, 22 November 2024
Back to Electricity_and_Magnetism
Textbook
Introduction
Ferromagnets and Electromagnets
Materials such as iron, cobalt, and nickel exhibit strong magnetic properties due to the alignment of their atomic magnetic moments. Ferromagnetic domains align to create a net magnetic field. Electromagnets use electric current to generate a magnetic field. The magnetic field strength is proportional to the current and the number of coils. All magnets have a north and south pole. Unlike poles attract and like poles repel. It is impossible to separate north from the south poles.
The magnetic properties of materials arise from:
- The spin of electrons,
- The orbital motion of electrons around the nucleus.
Application of Ferromagnets and Electromagnets include:
- MRI machines
- Data Storage (Hard drives, Audio Tape)
- Electric motors
Earth's Magnetic Field
Magnetic Field Lines
Magnetic field lines represent the direction and strength of the magnetic field. Magnetic field lines go from the north pole to the south pole of a magnet (the direction a compass would point). The form loops and never cross.
Motion of a Charged Particle in a Magnetic Field
Force on a Moving Charge
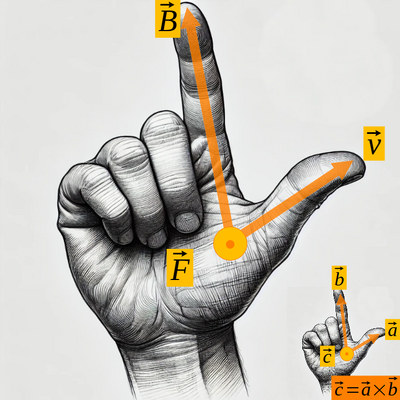
The force on a moving charge in a magnetic field is given by the Lorentz force:
- Formula:
Where: * is the velocity of the charge, * denotes the cross product.
Applications
Northern Lights
Charged particles from the solar wind are guided by the Earth's magnetic field, exciting atmospheric gases and producing visible light.
Van Allen Belt
Regions of trapped charged particles in the Earth's magnetic field. These particles spiral along magnetic field lines.
Mass Spectrometer
Used to measure the mass-to-charge ratio of ions.
Cyclotron
A type of particle accelerator that uses a perpendicular magnetic field to accelerate charged particles in a circular path.
Combined Fields
Force on a Moving Charge due to Electric and Magnetic Fields
The force on a charge moving in both electric and magnetic fields is:
- Formula:
Thomson Experiment (Discovery of the Electron)
Used crossed electric and magnetic fields to determine the charge-to-mass ratio of the electron.
Hall Effect
The creation of a voltage difference across an electrical conductor, transverse to the electric current and the applied magnetic field.
Magnetic Force on a Current-Carrying Wire
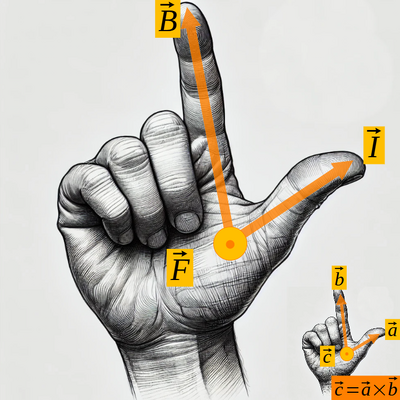
The force on a wire of length carrying current in a magnetic field is:
- Formula:
Torque on a Current Loop - the Electric Motor
A current loop in a magnetic field experiences torque, which is the basis for electric motors.
- Formula:
Where: * is the torque, * is the number of loops, * is the current, * is the area of the loop, * is the magnetic field, * is the angle between the magnetic field and the normal to the loop.
Magnetic Dipole
A magnetic dipole consists of a closed loop of electric current or a pair of opposite magnetic poles separated by a distance. The magnetic moment is a vector quantity that points perpendicular to the plane of the current loop and is proportional to the current and the area of the loop:
- Formula:
Where: * is the magnetic dipole moment, * is number of turns, * is the current, * is the area of the loop, * is a unit vector perpendicular to the loop, following the right-hand rule.
- Right-hand rule**: Curl the fingers of your right hand in the direction of the current around the loop. Your thumb will point in the direction of the magnetic dipole moment .
Torque on a Magnetic Dipole in a Magnetic Field
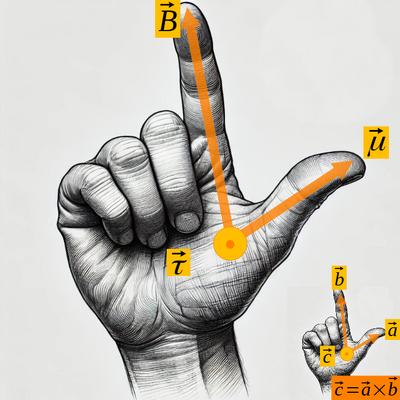
When a magnetic dipole is placed in an external magnetic field , it experiences a torque , which tends to align the dipole with the field:
- Formula:
Where: * is the torque, * is the magnetic dipole moment, * is the magnetic field.
Potential Energy of a Magnetic Dipole
The potential energy of a magnetic dipole in a magnetic field is given by:
- Formula:
Where: * is the potential energy, * is the magnetic dipole moment, * is the magnetic field.
The potential energy is minimized when the dipole is aligned with the magnetic field, and maximized when it is opposite to the magnetic field.
Simulations
Understanding the earth's magnetic field:
- Bar Magnet and compass
- Earth's magnetic Field
- demo of magnetic field lines with iron filings (one magnet)
- demo of magnetic field lines with iron filings (two magnets)
Vector Product:
Back to Electricity_and_Magnetism
Next: Sources of Magnetic Fields - Biot Savart