Sources of Magnetic Fields - Biot Savart

Back to Electricity_and_Magnetism

Textbook

• University Physics Volume 2: Chapter 12 - Sources of Magnetic Fields

Magnetic fields due to current in a wire

Biot-Savart: The general equation for the magnetic field due to a section of a wire

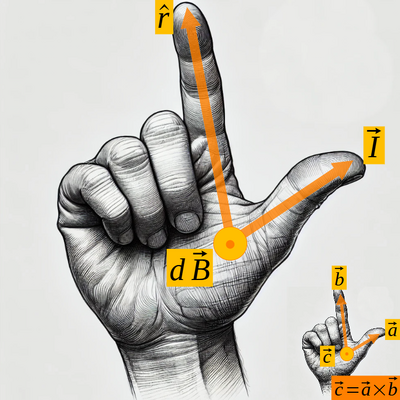
The magnetic field produced by a small segment of a current-carrying wire can be calculated using the Biot-Savart Law. This law relates the magnetic field ${\vec {dB}}$ produced by an infinitesimal section of current-carrying wire $d{\vec {l}}$ to the current $I$ and the distance $r$ from the segment:

$d{\vec {B}}={\frac {\mu _{0}}{4\pi }}{\frac {Id{\vec {l}}\times {\hat {r}}}{r^{2}}}$

Where:

• $\mu _{0}=4\pi \times 10^{-7}\,{\text{T}}\cdot {\text{m/A}}$ is the permeability of free space,
• $d{\vec {l}}$ is the infinitesimal vector length of the wire,
• ${\hat {r}}$ is the unit vector pointing from the wire segment to the point of interest,
• $r$ is the distance from the wire segment to the point of interest.

Biot Savart: Particular Solutions

Often, it is not necessary to integrate the general Biot-Savart Law (ask your teacher if you have to be able to), instead the particular solutions that follow can be used.

Magnetic field due to a finite straight wire

The magnetic field at a point due to a finite straight wire carrying a current $I$ can be calculated using the Biot-Savart Law. For a finite wire of length $L$, the magnetic field at a point $P$ located at a perpendicular distance $r$ from the wire (with the wire making angles $\theta _{1}$ and $\theta _{2}$ at the point) is given by:

$B={\frac {\mu _{0}I}{4\pi r}}\left(\sin \theta _{1}+\sin \theta _{2}\right)$

Where:

$\mu _{0}=4\pi \times 10^{-7},{\text{T}}\cdot {\text{m/A}}$ is the permeability of free space, $I$ is the current flowing through the wire, $r$ is the perpendicular distance from the wire to the point where the magnetic field is being calculated, $\theta _{1}$ and $\theta _{2}$ are the angles that point to the ends of the wire from the point of interest.

Magnetic field due to an infinite straight wire

A special case of the above is an infinitely long, straight wire carrying a current $I$. The magnetic field at a distance $r$ from the wire is given by:

$B={\frac {\mu _{0}I}{2\pi r}}$

Where:

• $B$ is the magnitude of the magnetic field,
• $r$ is the distance from the wire,
• $I$ is the current in the wire.

The magnetic field forms concentric circles around the wire, and its direction can be determined using the right-hand rule.

This equation could also be found based on Ampere's-Law.

Magnetic field due to circular arc of wire

For a current-carrying circular arc of radius $R$ subtending an angle $\theta$ at the center, the magnetic field at the center of the arc is given by:

$B={\frac {\mu _{0}I\theta }{4\pi R}}$

Where:

• $I$ is the current through the arc,
• $\theta$ is the angle subtended by the arc at the center (in radians),
• $R$ is the radius of the arc.

This formula is derived from the Biot-Savart Law for a symmetric circular geometry.

Here’s a new section for the magnetic field due to a solenoid, formatted with Wiki math tags and covering both the case of a long solenoid (diameter much smaller than length \(L\)) and the general case:

Magnetic field inside a solenoid

The magnetic field inside a solenoid, which is a coil of wire with many turns, depends on the current flowing through the wire and the geometry of the solenoid.

For solenoids with diameter << length

In the case of a long solenoid with length L and a large number of closely spaced turns n (turns per unit length), the magnetic field inside the solenoid is approximately uniform and directed along the solenoid’s axis. The magnetic field inside the solenoid is given by:

$B=\mu _{0}nI$

Where:

• $\mu _{0}=4\pi \times 10^{-7}\,{\text{T}}\cdot {\text{m/A}}$ is the permeability of free space,
• $n$ is the number of turns per unit length of the solenoid ($n={\frac {N}{L}}$ for a solenoid with N turns and length L),
• $I$ is the current flowing through the solenoid.

This formula assumes that the magnetic field outside the solenoid is negligible and that the field inside is nearly uniform.

Solenoid in general

For a solenoid with diameter not negligible compared to its length, the magnetic field can be calculated as:

$B={\frac {\mu _{0}NI}{\sqrt {L^{2}+D^{2}}}}$

Where:

• $N$ is the number of turns,
• $L$ is the length of the solenoid,
• $D$ is the diameter the solenoid,
• $I$ is the current through the solenoid.

This result requires calculus and is used when the solenoid length cannot be approximated as infinite relative to its radius.

In both cases, the magnetic field direction follows the right-hand rule: if you curl the fingers of your right hand in the direction of the current winding in the solenoid, your thumb will point in the direction of the magnetic field along the solenoid's axis.

Adding up fields

When calculating the total magnetic field from multiple current elements, use the principle of superposition. The total magnetic field ${\vec {B}}_{\text{total}}$ is the vector sum of the individual fields ${\vec {B}}_{1}$, ${\vec {B}}_{2}$, ... from each current element:

${\vec {B}}_{\text{total}}={\vec {B}}_{1}+{\vec {B}}_{2}+\dots$

This requires adding the magnetic field vectors, taking into account both their magnitudes and directions.

Force between parallel wires

Two parallel wires carrying currents $I_{1}$ and $I_{2}$, separated by a distance $r$, exert a force on each other due to the magnetic fields they produce. The force per unit length between the wires is given by:

$F_{\text{per unit length}}={\frac {\mu _{0}I_{1}I_{2}}{2\pi r}}$

Where:

• $I_{1}$ and $I_{2}$ are the currents in the wires,
• $r$ is the separation between the wires.

The force is attractive if the currents are in the same direction and repulsive if the currents are in opposite directions.

Back to Electricity_and_Magnetism