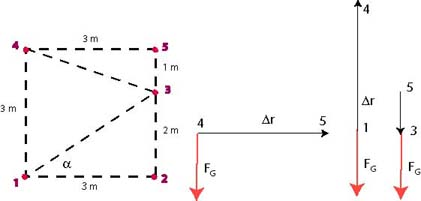
Work EX 7

The weight of the block is 15 N. To find the work done by gravity we have to determine the angle $\theta$ between vectors $F_G$ and $\mathrm{\Delta }r$ so that we can compute the work $W_{F_G}=F_G\mathrm{\Delta }rcos\theta$. Or we can work with components of these vectors and write $W_{F_G}=F_x{r}_x+F_y{r}_y$. There is another way to look at it: The work is a product of the magnitude of the force and the component of the displacement parallel to the force. This is because the work done along the path perpendicular to the force is zero.

(a) In the first problem we see that the displacement from 1 to 3 has a component pointing "up" (dashed lines) which is parallel to the force and a component pointing to the "right" which is perpendicular to the force. The work done along this path is zero while the work done along the path pointing "up" is $(15)(2)\cos (180^{\circ })=-30J$. Therefore $W_{13}=-30J$. You may check it out numerically by computing $\theta =\arctan (2/3)$ and then using the familiar equation for the work.

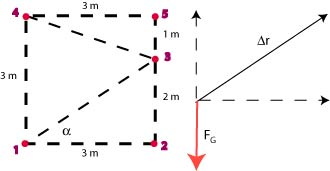
(b) The work done along the path $12$ is zero because the path is perpendicular to the force. The work done along the path $23$ is $W_{23}=(15)(2)\cos (180^{\circ })=-30J$. The answer is the same as in (a): $W_{12}+W_{23}=-30J$

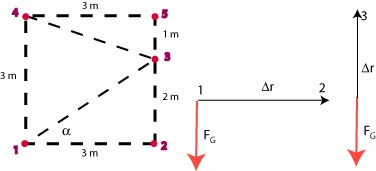
(c) The work done along the path $14$ is $W_{14}=(15)(3)\cos (180^{\circ })=-45J$ and the work done along the path $45$ is zero because the path is perpendicular to the force. Therefore $W_{14}+W_{45}=-45J$.

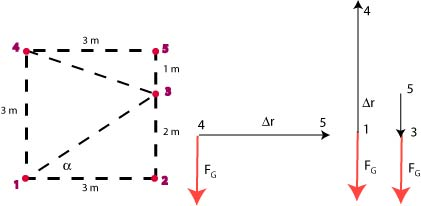
(d) In this problem, we are left to compute the work done along the path $53$. The displacement points in the same direction as the force: $W_{53}=(15)(1)\cos (0^{\circ })=15J$. Therefore $W_{14}+W_{45}+W_{53}=-45+0+15=-30J$. Note that the answer is the same as in the questions (a) and (b).