Work-Energy Theorem EX 4

The diagram below shows our understanding of the situation. There are two forces acting on a bucket of water: $F_G$ and $F_T$. The tension in the rope lifts the water up. Therefore, the question in this problem is to find the work done by the tension. We choose the x-axis parallel to the displacement and thus the x-component of the displacement is $\mathrm{\Delta }x=12m$.

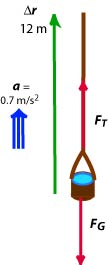
We can determine the net work because we know the acceleration, which is related to the net force:

${F_{net}}_x=ma=(15)(0.7)=10.5N$

Consequently, the net work is

$W_{net}={F_{net}}_x\mathrm{\Delta }x=(10.5)(12)=126J$

Since the net work is the sum of the work done by gravity and by the tension ($W_{net}=W_{F_T}+W_{F_G}$) we can find the work done by tension by first finding the work done by gravity. The x-component of the gravitational force is ${F_G}_x=150\cos (180^{\circ })=-150N$:

$W_{F_G}=(-150)(12)=-1800J$

From the net work and the work done by gravity, we find

$W_{F_T}=W_{net}-W_{F_G}=126-(-1800)=1926J$