Torque EX 1

(a) The diagram shows the force acting on the meterstick, the pivot (black dot) and the lever arm in case a). The magnitude of the force is 10 N. The magnitude of the lever arm is 1/3 m.

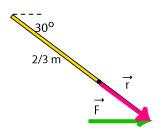
To solve this problem, we first move the force vector and the lever arm vector so that they are placed "tail to tail", then we draw the x-axis parallel to the lever arm and we determine the angle between them:

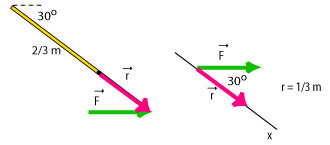
From the diagram we see that the angle $\theta$ that we will use in the equation for the torque is 30°.

Since we drew the vector of the force in the "first quadrant" we conclude that the direction of the torque is counterclockwise and therefore the torque is positive:

$\tau =Fr\sin {\theta }=(10)(0.33)\sin {30^{\circ }}=1.65Nm$

(b) The diagram shows the force acting on the meterstick, the pivot (black dot) and the lever arm in case b). The magnitude of the force is 10 N. The magnitude of the lever arm is 0 m since the force acts at the pivot. Therefore the torque is zero.

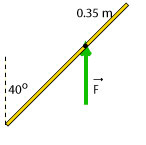
(c) The diagram shows the force acting on the meterstick, the pivot (black dot) and the lever arm in case c). The magnitude of the force is 10 N. The magnitude of the lever arm is 0.75 m.

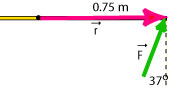
To solve this problem we first move the force vector and the lever arm vector so that they are placed "tail to tail", then we draw the x-axis parallel to the lever arm and we determine the angle between them.:

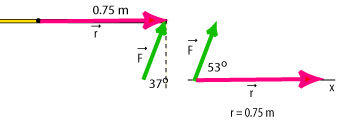
From the diagram we see that the angle $\theta$ that we will use in the equation for the torque is 53°.

Since we drew the vector of the force in the "first quadrant" we conclude that the direction of the torque is counterclockwise and therefore the torque is positive:

$\tau =(10)(0.75)\sin {53^{\circ }}=6Nm$

(d) The diagram shows the force acting on the meterstick, the pivot (black dot) and the lever arm in case d). The magnitude of the force is 10 N. The magnitude of the lever arm is 0.75 m. The line of force passes through the pivot point and therefore the torque is zero.

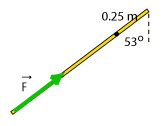
(e) The diagram shows the force acting on the meterstick, the pivot (black dot) and the lever arm in case e). The magnitude of the force is 10 N. The magnitude of the lever arm is 0.5 m.

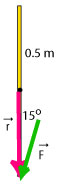
To solve this problem we first move the force vector and the lever arm vector so that they are placed "tail to tail", then we draw the x-axis parallel to the lever arm and we determine the angle between them:

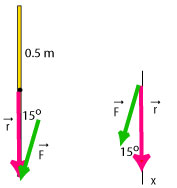
From the diagram we see that the angle $\theta$ that we will use in the equation for the torque is 15°.

Since we drew the vector of the force in the "fourth quadrant" we conclude that the direction of the torque is counterclockwise and therefore the torque is positive:

$\tau =(10)(0.5)\sin {15^{\circ }}=1.29Nm$