Torque

Helena Dedic

If you need to understand the concept of center of mass, please see the link below:
CENTER OF MASS

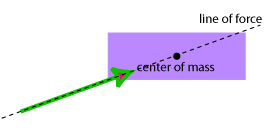
• A force causes a free object to move in a translational motion if it is applied at the centre of mass of the object or the line of force passes through the centre of mass.
  
  

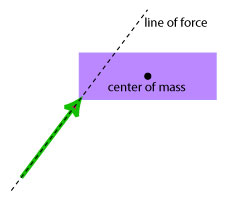
• When a force is not applied at the centre of mass of a free object or when the line of force does not pass through the centre of mass then it causes this object to move in a complex way that involves both translation (i.e.: movement of the center of mass) as well as rotation (i.e.: movement around the center of mass.)
  
  

• OBSERVATIONS OF AN OBJECT:

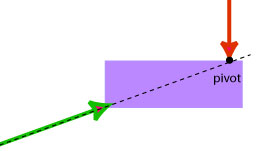
a) When a force acts at the pivot or when a line of force passes through the pivot, 

the object does not begin to rotate.

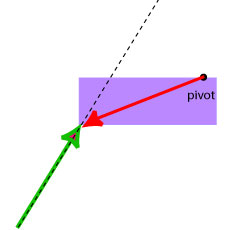
b) When a force acts at some distance from the pivot, the object begins to rotate.

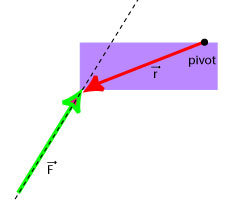
• Lever arm is a vector that points from the pivot to the point where the force acts.
  
  

• TORQUE: A cause of a change of the angular velocity (e.g.: a rotating wheel stops or it begins to rotate faster.

The symbol for torque is $\overrightarrow{\tau }$.

• Magnitude and direction of the torque: The magnitude of the torque depends on the magnitude of the lever arm, the magnitude of the force and the angle between these two vectors:

$\tau =\pm Fr\sin \theta$

In special cases where the axis of rotation is given: The torque is positive when the torque causes the object to rotate in the counter-clockwise direction and negative when the torque causes the object to rotate in the clockwise direction.

• In general the torque is a vector product of the lever arm and the force:

$\overrightarrow{\tau }=\overrightarrow{r}\times \overrightarrow{F}$

EXERCISES ON TORQUE

Static Equilibrium Revisited

• An object is in static equilibrium if and only if ${\overrightarrow{\tau }}_{net}=0$ and ${\overrightarrow{F}}_{net}=0$, where the net torque is the sum of all torques and the net force is the sum of all forces acting on an object.
  
  
• Static equilibrium problem solving strategy:
  
  

1. Determine all forces acting on an object and draw an arrow for each force indicating:
   • A point where this force is applied
   • In which direction this force acts
2. For each force:
   • Identify the magnitude and the direction of lever arm
   • Draw a diagram consisting of lever arm and force vectors and determine the angle between these two vectors
   • Determine the direction of the torque and then compute its magnitude.
3. Substitute into the equation $\mathrm{\Sigma }\tau =0$
4. Select the coordinate system
5. Draw a free-body diagram
6. Compute the components of the forces
7. Substitute into the equations $\mathrm{\Sigma }{F}_x=0$ and $\mathrm{\Sigma }{F}_y=0$
8. Solve the system of three equations using the method of substitution

EXERCISES ON STATIC EQUILIBRIUM