Static and Dynamic Equilibrium EX 4
We will consider the two boxes separately. The pulley and the string are massless and there is no friction on the pulley. Therefore we can consider that the tension in the string is constant.
Consider the mass kg:
The forces acting on are , , , . The normal force and force of friction are acting on this block because it is in contact with a surface. The force of friction acts uphill because the block moves downward and the friction opposes the slide between the two surfaces (the box and the incline).
Now we will consider the mass kg:
The forces exerted on are , . The force of friction and the normal force don't enter into consideration since this block is not in contact with any surface.
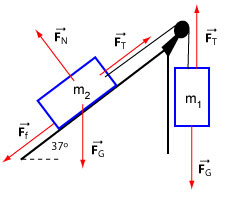
We will select a different system of axes for each of the blocks: x-axis pointing up along the incline for and x-axis pointing downward for . The x-axis points in the direction of motion in both cases.
The figure below shows these forces and free body diagrams for both particles.
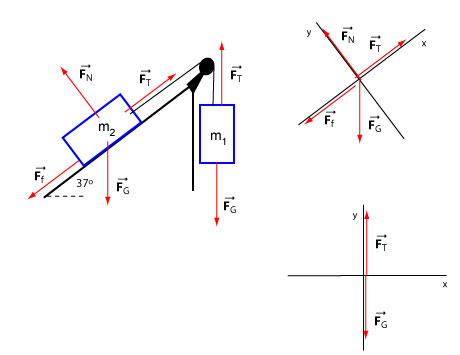
Let's compute the components first for block :
| Forces | x-component | y-component |
|---|---|---|
| 50 cos(-127°) = -30 N | 50 sin(-127°) = -40 N | |
| 0 | ||
| 0 | ||
| 0 |
Note that we used in our calculations.
Now we compute the components of the forces acting on :
| Forces | x-component | y-component |
|---|---|---|
| 50 | 0 | |
| 0 |
We deal first with the y-component for .
This yields N.
Now we write the equations for the x-component for
and for .
We can solve the second equation we find N. And then we find the magnitude of the force of friction N. Note that it is because of the force of friction that these two equal masses can move at constant velocity. Without friction the x-component of the gravitational force acting on is smaller than the x-component of the gravitational force acting on .