Static and Dynamic Equilibrium EX 1

Helena Dedic

The two blocks are at rest. It means that the blocks are in static equilibrium and that the net force on each block as well as the net force on the system of the two blocks is zero. The diagram below shows the system (dashed box).

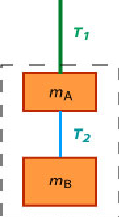
The upper rope exerts a force of tension on the system. This force cannot exceed 8 N.

${\vec {F_{T}}}\leq 8N$

The other force acting on the system of the two blocks is the weight.

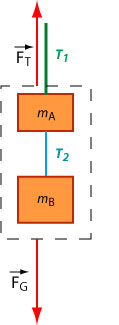
Since the sum of these two forces must be equal to zero, we conclude that the weight cannot exceed 8 N either.

${\vec {F_{G}}}\leq 8N$

Further, since the weight is equal $mg$, we conclude that the total mass of the system cannot exceed 0.8 kg and therefore the mass $m_{B}$ cannot exceed 0.6 kg.

On the other hand, the net force on each block must also be equal to zero.

If we consider the forces exerted on $m_{B}$ and note that the tension in the lower rope cannot exceed 4 N we can use a reasoning similar to the the one that we used for the system of the two blocks and conclude that the weight of the block $m_{B}$ cannot exceed 4 N.

Therefore the mass of the block $m_{B}$ cannot exceed 0.4 kg. Consequently, the maximum mass of the block $m_{B}$ is the lower of the two upper limits or 0.4 kg and the tension in the lower rope is 4 N.

Returning to our consideration of the system of two blocks, the maximum total mass of the system is 0.6 kg and the weight of the whole system is 6 N. Thus we conclude that the tension in the upper rope will also be 6 N.