Proj Motion EX 7

Helena Dedic

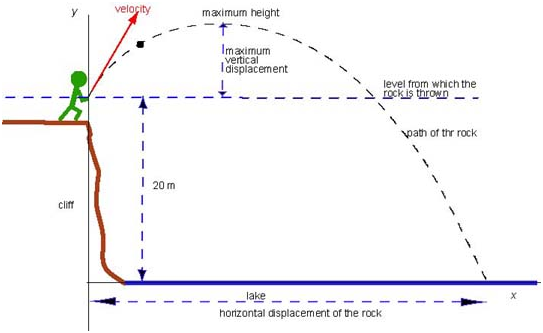
Jack, standing on a cliff, throws a rock into a lake 20 m below with initial velocity 25 m/s at 53° above horizontal.

a. How high above the water will the rock rise?

b. How far from the cliff (along horizontal) will the rock land?

c. With what velocity will it land?

Solution:

We will begin by verbalizing our understanding of the motion. A rock is thrown from a height of 20 m above the water. It has some velocity at the moment it leaves Jack's hand. The speed is 25 m/s.

Since the angle is above the horizontal, we know that both the x- and y-components are initially nonzero.

Furthermore, since the angle is above the horizontal, the rock will rise.

Let us choose our coordinate system before going any farther. Orient the positive y-axis vertically upward and the positive x-axis along the horizontal, pointing across the lake.

Put the origin at the level of the lake and just below the point where the rock was released. The initial position of the rock, in this coordinate system, is (0,20). Now, both the x- and y-components of velocity are initially positive. The x-component remains constant, while the y-component decreases at a rate of 10 m/s every second because the rock is in a free fall.

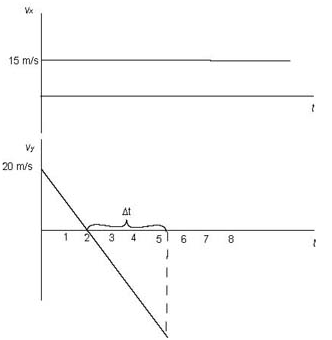
Since the x-component of the velocity is constant, the $v_{x}$ - t graph is a flat line. Since the y-component decreases at a rate of 10 m/s every second, the vertical velocity is zero when the rock rises to its maximum height and the rock will be speeding up towards the lake.

Although it is speeding up, its velocity is decreasing at the rate it was slowing down on the way towards its peak. The rock follows a parabolic path towards the lake. The $v_{y}$ - t graph is a straight line with positive "y-intercept" because the rock moves initially upward.

The slope of the straight line is $-10m/s^{2}$. We note that the rock, on its way down, covers the distance it has risen plus 20 m (the distance from the point of release to the water).

Consider the following picture:

Now we compute the components of velocity:

vx = 25 cos53° = 15 m/s

vy = 25 sin53° = 20 m/s

so that their graphs are as follows:

Since the slope is - 10 m/s2 the graph crosses the t-axis at t = 2 s. Therefore the rock takes 2 s to rise to its maximum height.

In those 2 s the rock rises ½ • 20 • 2 = 20 m. It then begins to move downward. It has to move 40 m to reach the lake. We don't know when the lake is reached but we will assume that it will take some $\Delta t$.

The area under this triangle should be equal to - 40 m and the height of this triangle is - 10 × $\Delta t$ given the slope of the graph. From the equation for the area we get ½ $\Delta t$ × (- 10 × $\Delta t$) = - 40.

Solving for $\Delta t$ we find 2.8 s.

This means that the rock will fall down for 2.8 s. The y-component of velocity at the moment when the rock splashes into the lake is shown by the dashed line in the diagram above. We note that it is - 28 m/s. It is negative because the rock is moving down.

Now we are ready to answer the questions:

a. How high above the water will the rock rise? It will rise 40 m above the water.

b. How far from the cliff (along horizontal) will the rock land? We don't yet know, but we know that it took 2 + 2.8 = 4.8 s to splash into the lake. Given that the horizontal velocity is always 15 m/s we compute the horizontal distance to be 4.8 × 15 = 42 m.

c. With what velocity will it land? The velocity has two components (15, - 28)m/s.

• Back to Projectile Motion
  
  
• Back to Exercises on Projectile Motion