Potential Energy EX 4

The block slides down the distance 3 m and then continues to slide down some more. Let's assume that it slides some further distance $x$. It means that the total distance the block moves down the incline is $3+x$. It moves down the height $h=(3+x)\sin(30^{\circ })$. The spring which was initially uncompressed is now compressed by $x$.

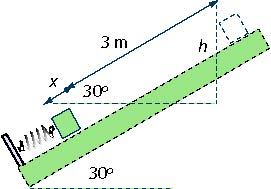
The question is to find the distance $x$ such that the total change in potential energy of the system (spring-block-Earth) is zero. To find this distance we will first compute the change of height from the triangle in the diagram above:

$\sin(30^{\circ })={h \over 3+x}$

$h=(3+x)\sin(30^{\circ })$

And then the change in gravitational potential energy using the equation:

$\Delta U_{G}=-mgh=-(0.1)(10)((3+x)\sin(30^{\circ }))$

And then compute the change in the spring's potential energy:

$\Delta U_{sp}={\frac {1}{2}}k{x_{f}}^{2}-{\frac {1}{2}}k{x_{i}}^{2}={\frac {1}{2}}kx^{2}$

The total change in potential energy is then

$\Delta U_{G}+\Delta U_{sp}=0$

$[-(0.1)(10)((3+x)\sin(30^{\circ }))]+[{\frac {1}{2}}(4)x^{2}]=0$

$-(3+x)+4x^{2}=0$

Solving the quadratic equation for $x$, we find $x=1$ m. Note that we select the positive solution since the distance is always positive.