Module : Work and Kinetic Energy

Kreshnik Angoni and Kevin Lenton
Worksheet.docx
Worksheet.pdf

Other Resources:

• Haliday & Resnick, Fundamentals of Physics 30.1-5
• Openstax
• Printable version

Two concepts, work and energy, are widely used when studying mechanics because they are scalar quantities and therefore much easier to work with (excuse the pun) than force (a vector). Especially, if the force changes (either magnitude, direction or both) during the object's motion (for example; the force of a spring , the normal or friction force along a curved surface), it is easier to use work and energy instead of Newton’s laws.
Consider the following scenario:
When lifting a body up with zero acceleration you have to exert a force with magnitude equal to that of the body's weight. Everyday experience shows that:
• For the same vertical distance moved, the bigger the weight is, the more muscular exertion is needed;
• For the same weight, the bigger the vertical distance moved is, the more muscular exertion is needed;
This shows that the quantity (force times distance) can be a meaningful measure to characterize the activity exerted by a “source” that moves up an object from one level to higher one. This essential information, intuitively confirmed, opens the way for the precise definition of mechanical work.
This is linked to the concept of energy, a first step approach would be to figure it out as the “capacity of a source to provide mechanical work”. This way of looking at energy means that “the work provided by a source should be equal to the change of energy in the source that provides it “ and this definition is good enough as long as we deal only with mechanical phenomena without heat production.
Work is energy transferred by a force.

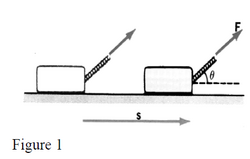
THE WORK DONE BY A CONSTANT FORCE

A constant force F. has done work only if the point where the force is applied moves.
If the object displacement is s , the force must also have moved by this amount and the work done is equal to:
$W={\vec {F}}\cdot {\vec {s}}=F\ s\ cos\theta \qquad \qquad \qquad (1)$

$\theta$ (constant) is the angle between the direction of force and the direction of displacement vectors.
Note that:
•The work is done by the source that exerts the force.
•If the displacement is zero, there is zero work even if the source makes an effort (applies the force).
•Only the component of the force along the displacement direction achieves work. The force component perpendicular to displacement achieves zero work because in this case $\theta =90^{\circ }$.

As it is defined by a scalar product, the work is a scalar physical quantity.
Its unit is a derived unit; in the SI system its unit is the Joule (J); 1J = 1N*1m (force applied in the displacement direction) (2)

You can calculate the work done by a constant force F during a displacement s by using the components of those vectors in any Cartesian frame through the formula :
$W={\vec {F}}\cdot {\vec {s}}=F_{x}\times s_{x}+F_{y}\times s_{y}+F_{z}\times s_{z}=F_{x}\Delta x+F_{y}\Delta y+F_{z}\Delta z\qquad \qquad \qquad (3)$

Remember a) ${\vec {F}}=F_{x}\mathbf {\hat {\imath }} +F_{y}\mathbf {\hat {\jmath }} +F_{z}\mathbf {\hat {k}}$ and ${\vec {s}}=x\mathbf {\hat {\imath }} +y\mathbf {\hat {\jmath }} +z\mathbf {\hat {k}}$ and
b) Rules of scalar product
  Meanwhile, the numerical value of work does not depend on the frame of reference, because the magnitudes of the vectors F , s and the angle between them (see expression 1) do not depend on any frame.

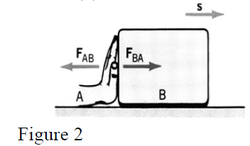
The work done by ${\vec {F_{G}}}$ or ${\vec {N}}$ when a block slides over a horizontal plane (fig.2) is zero because both these forces are both perpendicular to the displacement vector. For the same reason the work done by centripetal forces is always zero. When considering the work done by friction forces you have to verify carefully the directions of the displacement and the friction force vectors before starting any numerical calculations. In the case shown in fig 3.a the friction force on the block is opposite in direction compared todisplacement vector and $W_{f}={\vec {f_{k}}}\cdot {\vec {s}}=f_{k}\ s\ cos180^{\circ }=-f_{k}.s\qquad \qquad \qquad (4)$
So, the friction does negative work on the block. Note that the source of the friction force is the floor. In the case of figure 3.b, the force $F_{0}$ pushes the block B forward. Due to its inertia, the block A tends

to keep its motion status and this way it would tend to slide left over block B. Meanwhile, block B pulls A to the right via the friction force. In this case the (static or kinetic) friction force exerted on block A has the same direction as the displacement of A and its work is positive.
$W_{f}=+fk\ s$
When a set of forces $F_{1},F_{2},...,F_{n}$ is acting on the same body that is displaced by ${\vec {s}}$, each force does work independently of the forces.
$W_{1}={\vec {F_{1}}}\cdot {\vec {s}};W_{2}={\vec {F_{2}}}\cdot {\vec {s}}_{.}...........W_{n}={\vec {F_{n}}}\cdot {\vec {s}}$ (5)
The total work done on the object is
$W_{net}=W_{1}+W_{2}+..W_{n}=({\vec {F_{1}}}+{\vec {F_{2}}}+...{\vec {F_{n}}})\cdot {\vec {s}}={\vec {F_{net}}}\cdot {\vec {s}}\qquad \qquad \qquad (6)$

${\vec {F_{net}}}=\sum _{i}^{n}{\vec {F_{i}}}\qquad$ is the vector sum of all forces exerted on the body.
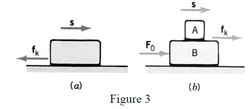
From (1) you can see that the work done by a force can be positive (if $\theta <90^{\circ }$ ) or negative (if $\theta >90^{\circ }$).<be> In figure 2, the hand “object A” pushes the block “object B” and moves it through the displacement s. This way, via the force exerted on B, “object A” does positive work
$W_{onBbyA}={\vec {F_{BA}}}\cdot {\vec {s}}=F_{BA}\ s\ cos0^{\circ }\qquad \qquad \qquad (7)$

The Newton's third law states that the force that block “object B “exerts on the hand “object A” is equal in magnitude but opposite in direction to ${\vec {F_{BA}}}$.
${\vec {F_{AB}}}=-{\vec {F_{BA}}}\qquad \qquad \qquad (8)$

The work done by the force of the block on the hand ( $W_{\vec {F_{AB}}}$ work) after the hand is moved by ${\vec {s}}$ is
$W_{onAbyB}={\vec {F_{AB}}}\cdot {\vec {s}}=-{\vec {F_{ABA}}}\cdot {\vec {s}}=-W_{onBbyA}\qquad \qquad \qquad (9)$

So, when object A (the hand) does positive work to move object B (the block), then object B (block) does the same amount of work (but negative) on object A, which is the “source of force that moves it”.

  The work done by the force of gravity is an important first step in introducing the concept of energy . Consider a block that is moved up an inclined plane under the effect of a pulling force (fig.4). Let’s ignore the action of other forces and concentrate on the work done by the weight. We define the displacement vector and select a frame of axes as shown. The selected system for the axes is not appropriate to study the motion using Newton's laws but it allows us to infer some important results and simplifies the calculation of work by gravity. The components of the force of gravity along these x,y coordinates are $F_{G_{x}}=0;F_{G_{y}}=-mg$ and those of the displacement are $s_{x}=\Delta x;s_{y}=\Delta y$.
So, equation (3) gives:
$W_{onBlockBbyGravity}=(0\mathbf {\hat {\imath }} -mg\mathbf {\hat {\jmath }} )\cdot (\Delta x\mathbf {\hat {\imath }} +\Delta y\mathbf {\hat {\jmath }} )=-mg\Delta y$

$W_{onBlockBbyGravity}=-mg(y_{f}-y_{i}\qquad \qquad \qquad (10)$

When the block is moved up, yf > yi and the work done by gravity on the block is negative. When the block slides down, yf < yi the work done by gravity on the block is positive.

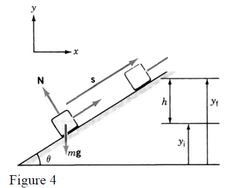
Note: If, initially, the block is moved up from height yi to yf and then left to slide down to yi , the total work done by gravity force on the block is zero.

$W_{G}^{up}+W_{G}^{down}=[-mg(y_{f}-y_{i})]+[-mg(y_{i}-y_{f})]$

$W_{G-total}=-mg\ [(y_{f}-y_{i})+(y_{i}-y_{f})]=0$

So: The work done by gravity depends only on the initial and final heights and not on the path followed during the displacement.
This means that, the work done by gravity is zero for any closed path (final location is the same as the initial location).

THE AREA TECHNIQUE FOR WORK CALCULATIONS IN ONE DIMENSION SPACE

For a constant force in one dimension space:
${\vec {F}}=F_{x}{\hat {\imath }}\ ;\ {\vec {s}}=x{\hat {\imath }}\qquad and\qquad W=F_{x}\Delta x=F(x_{f}-x_{i})\qquad \qquad \qquad (11)$

This work is equal to the shaded area under the graph f = f(x) shown in figure 5.a. If you set the origin at xi=0 then $W=F_{x}x_{f}$ corresponds to the area under the force graph from xi= 0 to x = xf.

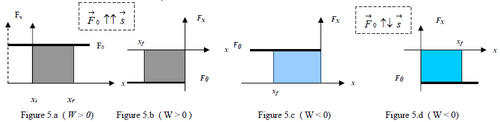
Note that when this area is located in first or third quadrant it is positive i.e. force and displacement are in the same direction, (both either positive or negative)work is positive ; when it is located in the second or fourth quadrant it does negative work ( fig.5.c, d)[the force is opposite to the displacement].

Work done by the Force of a Spring

The area technique offers an easy way for calculating work in the case of variable forces. In this case, the force has a different value for each location of the object under study. The elastic force of a spring is a good example of such type of force; when compressed or extended, an ideal (massless) spring, exerts an “elastic or restoring force” given by Hooke’s law: $F_{spring}=-kx\qquad \qquad \qquad (12)$
k [N/m] is the spring constant; x is the displacement from equilibrium; +x=extended; -x=compressed.

This expression assumes that xi = 0 (at the equilibrium position, the spring is unextended); in this way the displacement becomes equal to the algebraic value of x.
When x > 0 (spring extended) the force Fsp < 0 and when x < 0 (spring compressed) the force Fsp > 0. So, in any case, the spring’s force tends to restore the equilibrium position of spring. The forces that tend to bring the system to its equilibrium configuration are known as restoring forces.

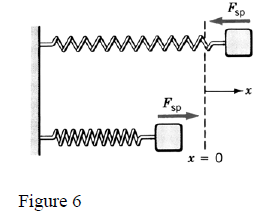
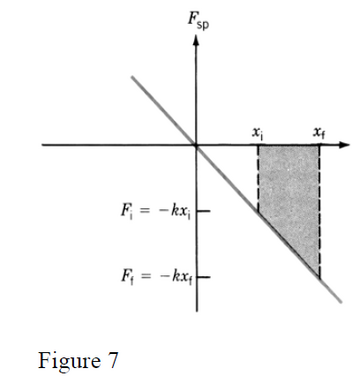
Figure 7 shows the graph of equation (12). The work done by elastic force when its application point (spring end) is shifted from xi to xf is given by the shaded area under the graph. By calculating this as the difference of the two triangle areas one finds out that
$W_{spring}=(-kx_{f}{\frac {x_{f}}{2}})-(-kx_{i}{\frac {x_{i}}{2}})={\frac {k}{2}}(x_{i}^{2}-x_{f}^{2})\qquad \qquad (13)$
In general, the work done by a spring is often written as $W_{spring}={\frac {1}{2}}kx^{2}$, just remember it is always the change that is important.
Expression (13) shows that the work done by a spring force (an elastic force) depends only on the initial and final positions of its moving end. The work done by a spring is positive when the direction of its force is the same as that of displacement. This happens when the block is moving towards the equilibrium point, i.e. when $|x_{i}|>|x_{f}|$

The spring’s work is negative when the direction of the restoring force is opposite to that of displacement. This happens when the block is moving away from the equilibrium point, i.e. when $|x_{i}|<|x_{f}|$

Also, for a full oscillation, the spring’s work is zero because xf = xi (the spring comes back to its initial position).
Note: The area technique may be used for any variable force but you should keep in mind that the sign of the area (i.e. work sign) under the graph depends on the location of starting point versus the location of final point. The sign of “areas” in figures 5.a,b,c,d is related to the location of starting point at x = 0.

THE WORK – ENERGY THEOREM

Consider a particle (an object) with mass m in translational motion with acceleration a along the x-direction under the effect of a net constant force ${\vec {F}}_{NET}$ directed along the same direction. The work done by the force ${\vec {F}}_{NET}$ for the displacement of the particle by $\Delta x=x_{f}-x_{i}$, is
$W_{NET}=F_{NET}\cdot \Delta x=(ma)*\Delta x=m*(a\Delta x)\qquad \qquad \qquad (14)$

By using the kinematic relationships between initial and final velocities you get:
$v_{f}^{2}-v_{i}^{2}=2a\Delta x\rightarrow a\Delta x={\frac {1}{2}}v_{f}^{2}-{\frac {1}{2}}v_{i}^{2}\qquad \qquad \qquad (15)$
and by substituting in eq. (14)
$W_{NET}={\frac {1}{2}}mv_{f}^{2}-{\frac {1}{2}}mv_{i}^{2}\qquad \qquad \qquad (16)$

Definition of Kinetic Energy

The quantity
$K={\frac {1}{2}}mv^{2}\qquad \qquad \qquad (17)$
is called the KINETIC ENERGY of the particle.
This means that you can express the work WNET done by the net force FNET through a difference of kinetic energy.
$W_{NET}=\Delta K=K_{f}-K_{i}\qquad \qquad \qquad (18)$

The Work-Kinetic Energy Theorem

Equation (18) is the mathematical expression of the Work-Kinetic Energy theorem (or simply the Work-Energy Theorem) which states that:

The net work done on a particle is equal to the change of its kinetic energy.

So, the energy is defined as a mathematical function whose change is equal to physics concept of work. Equation (17) shows that the numerical value of the kinetic energy does depend on the frame of reference. In another frame of reference (in uniform motion versus a first one), the velocity of the particle is different and therefore so is its kinetic energy. This helps to keep in mind that the numerical value of kinetic energy is not very meaningful. However, the change of kinetic energy is independent on the reference frame and does have a precise physical meaning; it is equal to the net work done on the particle.
For problems related to our experience here on earth, you could use an inertial frame tied to the earth. In this case, the kinetic energy of the terrestrial object is the work needed to increase its speed from zero to the given value ( put Ki = 0 in eq. (18) and get $W_{NET}=K_{f}={\frac {1}{2}}mv_{i}^{2}$ ).
In the same way, consider the situation when the object velocity is decreased from v to zero due to the stopping force external to the object. In this case, Kf = 0 and the net work done on the object is negative
$W_{NET}=-K_{f}=-{\frac {1}{2}}mv_{i}^{2}$

Remembering the third law, one infers that in this case, the object under consideration does positive work on the surrounding medium and in doing so it loses some of its kinetic energy. Note that this assertion is consistent with the idea about the energy as the capacity of this particle to provide work.

Important note: We derived the work-energy theorem for the case of constant force acting in a one-dimensional space. This theorem remains true in all cases, that is:
-variable forces

-acting in a two or three-dimensional space.  

POWER

Suppose that one needs to shift an object from point A to point B. This requires providing a certain amount of work and one has to choose between different sources that can provide this amount of work. Which one to chose? If one decides to use “the source that achieves faster displacement” one has to consider another physical quantity; the mechanical power.

The mechanical power is the rate at which a given work is done. If the “source” delivers a portion of work $\Delta W$ in the time interval $\Delta t$, you can say that it is delivering an average power equal to:
$P_{average}={\frac {\Delta W}{\Delta t}}\qquad \qquad \qquad (19)$

Units of Power

The unit of power in SI system is the “Watt “ 1W = 1J /1s (20)

Note: In the car industry anoth widely used unit of power is ”horsepower”; 1hp = 745.669W

The instantaneous mechanical power is defined as
$P=lim_{|Deltat\rightarrow 0}{\frac {\Delta W}{\Delta t}}\equiv {\frac {dW}{dt}}\qquad \qquad \qquad (21)$
We may assume that the “source” is acting on the object with a constant force F during an infinitesimal displacement ds. This means that it has provided the work
$dW={\vec {F}}\cdot d{\vec {s}}\qquad \qquad \qquad (22)$
If this happens during the infinitesimal time interval dt, it means that the object was moving with an instantaneous velocity
${\vec {v}}={\frac {d{\vec {s}}}{dt}}(23)$
from which we derive $d{\vec {s}}={\vec {v}}dt$

After substitution in (22) we get
$dW={\vec {F}}{\vec {v}}dt\qquad \qquad \qquad (24)$

and finally, based on (21)
$P={\frac {dW}{dt}}={\vec {f}}\cdot {\vec {v}}\qquad \qquad \qquad (25)$
The expression (25) is based on instantaneous vectors (force and velocity). Note that the power is a physical parameter that may change in time. But, if the force and velocity are constant vectors, the power is constant, too. In this case, the source provides a constant power in time.
From a formal point of view, the work done by the source of the force on an object can be seen as the portion of mechanical energy transferred from the “source to the adjacent regions of space”. This way, the delivered power [watt] from a “source” would be expressed as
$P=-{\frac {dE}{dt}}\qquad \qquad \qquad (26)$

where E [Joules] stands for the total mechanical energy of the “source” that provides the mechanical power . The sign “ - “ in expression (26) is related to the fact that the energy of the source is decreased when providing energy. The power received by the object is positive in the sense that positive work was done on the object.