Electric Current

Kreshnik Angoni and Kevin Lenton
Worksheet.docx
Worksheet.pdf

Additional Problems

Other Resources:

• Haliday & Resnick, Fundamentals of Physics 26.1-7
• Openstax
• Printable version

In electrostatics experiments, the electric charges move from one location to another (by friction, mechanical transport or by induction) but this movement lasts for a short interval of time. The next step in electricity is related to situations where the motion of charges lasts for a long time. One says that an electric current is produced if a non- zero net electric charge passes through a surface.

Attention: When a neutral fluid (like $H_{2}O$) flows through a hose, its molecules pass continuous across any hose section. So, there is a continuous movement of positive charges (p+) through hose section but the same quantity of negative charges (e-) passes (the H2O molecule is electrically neutral) simultaneously and there is no current because the net charge passing through the section is zero.

There are three main situations when an electric current is produced:

1. Free electrons in a conductor (e.g. a wire). In the absence of any electric field, the electrons move inside the conductor irregularly and the net charge passing any selected section is zero. In the presence of an E field, they move in the opposite direction to the field and produce a current.
2. The ions in an electrolyte (battery). The electrolytic solution in a battery contains positive and negative ions that have irregular movement (current zero) as far as the battery is not connected to a closed circuit. When the battery is connected to a closed circuit, these ions get a regular movement and a build a current inside the battery. A similar situation happens when it is produced a regular motion of ions inside a sample in “plasma” state.
3. The free charges (electrons e-,protons p+, ions) in vacuum. This is the case of e- used in a screen (oscilloscope, TV,.) or e- and p+ in an accelerator and ionic beams in different bombarding experiments.

Alessandro Volta performed the first experiments with electric current in 1799. Also, he built the first battery (voltaic pile) and used it in a closed circuit to heat wires enough that they glowed.

Definition of Current (I)

Let’s consider the flow of a net positive charge through a surface (Fig.1).

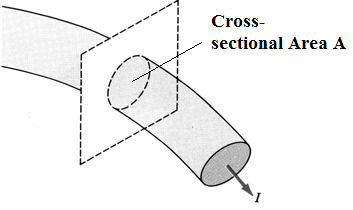
Assume that the net electric

charge $\Delta Q$ passes through the surface during the time interval $\Delta t$.
Then, the net charge passing through it during 1 sec, i.e. the average current, is

$I={\frac {\Delta Q}{\Delta t}}$

If the charge flow is not steady, one may refer to an infinitesimal interval of time dt and use the instantaneous current $I={\frac {dQ}{dt}}$

This expression shows that the electric current is the flow rate of net charge through a surface. The unit of current in SI system is 1Ampere (1A=1C/1s). Note that the current is a scalar (not a vector). The current follows the wire direction when propagating through a wire. By definition, the current starts at the positive terminal of the source (battery) and flows through circuit versus the negative terminal (Fig.2).

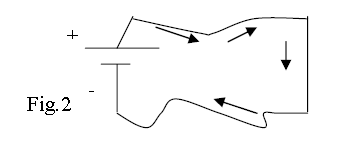
Fig.2

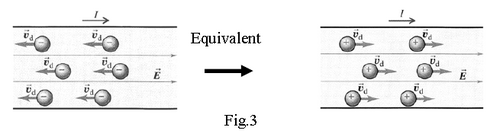
The convention is to define the direction of positive current as the direction of the positive charge flow. This means that in the case of conductors (wires, resistors,..) the direction of the current is opposite to the electron movement. Note that with this definition the current moves from higher potentials to lower potentials (downhill) and this simplifies the calculations for electric circuits. So, whenever the moving charge is “-Q”, one refers to the motion of charge “+Q” in opposite direction at the same speed (Fig.3).
In the case of the electrolyte inside a battery, there are both + and - charges present. The opposite-charge ions move in opposite directions and there are two components that add together to build the net current inside; one due to positive ions (moving along the current direction) and another one due to negative ions (moving in opposite direction to the current).

A wire is constituted by a metallic conductor (Cu, Al,.). As long as it is not connected into a circuit the free electrons inside the wire move irregularly. If only one of wire ends is connected to one of battery terminals, “some charges pass to the wire” and build the same potential ($=V_{terminal}$) on each wire point. The wire is yet in the frame of conductor electrostatics (static charge); there is only a field perpendicular to the wire surface and all charges are located “at rest” on its surface. If the other wire end is connected to the other battery terminal (in a closed circuit fig.2), the free electrons find themselves under an electric field due to difference of potential exerted between the two ends of wire. This field makes them move in opposite direction to the field and produce this way an electric current (opposite to their motion) along the field direction. Note that while the current flows, the net charge of the wire does not change because the same numbers of electrons that get into it through one terminal go out of wire from the other terminal.

A Model of Charge Movement: Current Density J and Drift Velocity ${\vec {v_{Drift}}}$

Most metal atoms are contained in a lattice/crystal structure. This often means that some of the electrons are free to move about the metal crystal. It is these free electrons which allow conductors to conduct charge (and also to conduct heat).
These electrons have kinetic energy and jump around randomly with some velocity. When an electric field is applied, these electrons start reacting to the field, and move against the field because they are negative. Their new net velocity is termed the drift velocity ${\vec {v_{Drift}}}\ or\ {\vec {v_{D}}}$. (Net because the electrons are still jumping around quite a bit due their own energy).

The electric current is defined with respect to the net charge that passes through a cross-section of a conductor. Note that, the current value does not depend on the value of the cross-sectional area that the current passes through. Sometimes you need to know about the charge flow at different locations inside the wire, at a specific point on the cross-section. The current density is the physical parameter that contains this information.
Consider a beam of “+” charged particles which move with the same velocity ${\vec {v_{Drift}}}\ or\ {\vec {v_{D}}}$ in the same direction as the current. Assume that each particle carries the same charge (+q) and all together move inside a cylinder with cross-section A. If n is the volume density of these charges (=the number of free electrons in the conductor ~$10^{29}electrons/m^{3}$), then there are $nlA$ charges inside the cylinder with length l; i.e. # of electrons= (electrons/volume) times volume), as shown in the figure:

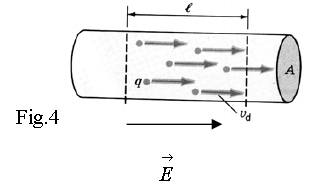
All these charges have passed through the section A after the interval of time
$\Delta t={\frac {l}{v_{D}}}$
Now the total charge will be
$\Delta Q=n\times l\times A\times q$

passes through the section A for time $\Delta t$, this means the current is

$I={\frac {\Delta Q}{\Delta t}}={\frac {nlAq}{l/v_{D}}}=nqv_{D}A$  
The average current per unit of section surface J is called current density

$J={\frac {I}{A}}={\frac {nlAq}{A}}=nqv_{D}$

The unit of current density in SI system is $A/m^{2}$ . Actually, the current density is defined as a vector ${\vec {J}}=nq{\vec {v_{D}}}$ Note that ${\vec {J}}$ may have different direction at different points of the same section crossed by a current. For negative charges the vector ${\vec {J}}$ has the opposite direction to ${\vec {v_{D}}}$ due to the negative sign of q.
Remember: The current is a scalar but the current density is a vector. The current is a macroscopic parameter; the current density is a microscopic parameter.

RESISTANCE (R) AND RESISTIVITY $\rho$

Experiments carried out with conducting objects show that: when one applies a difference of potential V at object ends, the current I passing through the object is proportional to V. The value of proportionality constant depends on the material, geometry and V&I range, but in all cases a relation of type I =cV holds. The resistance of a conductor object is defined as the inverse of this constant “c”.
So,

$R={\frac {V}{I}}$

This is Ohm's Law
Unit of Resistance: 1ohm($\Omega$) = 1V/1A) (8)

The resistance of a conductor defines how many volts one must apply at two ends so that 1A current passes through the conductor.

In normal conditions, the free electrons inside a neutral conductor move irregularly due to their thermal energy at a speed up to one million m/s. When a potential difference is applied, the electric field gives them an ordered movement against the field. This ordered motion is kept “under control” by the simultaneous increase of e- “collisions” to positive ions that form the crystal lattice. It turns out that the magnitude of the directed velocity ${\vec {v_{D}}}$ is very small (~ few cm/s). Its precise value depends on the E field magnitude and the crystal lattice ion density. The effect of the electric field on free electrons in a conductor results in an increase in the drift velocity. This is because, the magnitude of this velocity ${\vec {v_{D}}}$ is proportional to magnitude of local field in the wire
$|{\vec {v_{D}}}|\propto |{\vec {E}}|$

Referring to direction of motion for (+) charges and using equation(7) one may see that
${\vec {J}}\propto {\vec {v_{D}}}\propto {\vec {E}}$.
The precise relation between local current density and the local electric field is written in this form
${\vec {J}}={\frac {1}{\rho }}{\vec {E}}=\sigma {\vec {E}}$

The constant $\rho$ is the resistivity [units $\Omega {\dot {m}}$]and $\sigma (=1/\rho )$ is the conductivity of conductor.

Resistivity is a property of the material that constitutes the conductor. Consider again fig.4 and assume that the electric field is uniform in the small piece of wire. Then the potential difference across the ends of length l is

$V=E\times l$

From this we get E =V / l and, after substituting this into:
$J={\frac {E}{\rho }}={\frac {V}{\rho \ l}}$
we find out that
$I=J\ A={\frac {V}{\rho \ l}}A$
Using I=V/R and the above expressions you can show that:
$R=\rho {\frac {l}{A}}$

where $\rho$=resistivity; $l$=wire length; $A$=wire cross-sectional area

Therefore the Resistance of a cylindrical wire (=most common) of radius r and length l is:

$R=\rho {\frac {l}{\pi \ r^{2}}}$

Putting it all together: OHM’S LAW

In general, the resistance R of a conductor (defined as R = V/I ) has a value that depends on V and I.
(Note that there are many cases when it does not depend on V, I values e.g. thermistor)
Ohm’s law applies for all devices where R is a constant and it says:

The difference of potential V across the device is directly proportional to the current through it
$V=I\ R$
Remember: This relation for Ohm’s law only holds if R is constant and independent of V and I.

A material that obeys to Ohm’s law is called an ohmic material.
Provided the temperature is kept constant, all metals are ohmic materials. Carbon and some alloys behave as ohmic materials even when the temperature varies over a wide range. This explains why carbon is used to build high quality resistors. A resistor is a device used to provide a specified resistance in an electric circuit. A general-purpose resistor can be made using wire (in circuitry) or ceramic (in a stove-top element).

POWER IN A DC CIRCUIT

REMEMBER: When the force of gravity (=weight) pulls an object down an inclined plane (from high point to low point), the component of the weight does positive work W. This positive work, done by internal forces to the object-earth system, decreases the potential energy of object. If Uhigh and Ulow are the initial and final potential energies of the object, then the earth gravitational field delivers the work
$W_{int}=-\Delta U=-(U_{low}-U_{high})=(U_{high}-U_{low})$ .

Similarly, the electric field in a conductor moves the charge +q along its direction and this way builds the current inside the conductor. So, the electric field delivers a positive work “Wint” while shifting the charge q(+) from a higher to a lower potential point. This work can be expressed through the initial and final potential energies of the charge q in the field
$W_{int}=-\Delta U=-(U_{low}-U_{high})=(U_{high}-U_{low})=(V_{High}-V_{Low})\ q$

Note: In electric circuits, one often uses the notation V for the difference of potential $(V_{High}-V_{Low})=\Delta V=V$
During an infinitesimal interval of time dt, the electric field moves the amount of charge dq through the circuit and delivers the infinitesimal energy (as mechanic work or other energy forms)

$dU=V\ dq$
So, the electric field provides a power ( i.e. delivers energy at a rate) $P={\frac {dU}{dt}}=V\ {\frac {dq}{dt}}=V\ I$

This defines the power dissipated in a circuit.
For the case of a resistor, you can substitute V=IR to give:

$P=V\ I=I^{2}\ R={\frac {V^{2}}{R}}$ 

As explained, the electric field delivers work to move electrons in an ordered way and thus builds a current I. Let’s consider that an electric device is connected in the circuit shown below.

1. If the device is a resistor, all the energy delivered by the field is transferred into thermal energy. As electrons move at a constant drift velocity $v_{D}$, their average kinetic energy remains constant. So, once they gets to speed $v_{D}$, it transfers all the energy provided by field to ions of crystal lattice of resistor via collisions. This energy transfer increases the temperature of the resistor.
2. If the device is an electric motor, the energy delivered by the electric field is mainly transferred into mechanical work provided by the electric motor.
3. If the device is a recharging battery, the energy delivered by electric field is mainly transferred into chemical energy.
   
   

Note that in almost all cases some of the “electric energy” is transferred into thermal energy.

  The general law of energy conservation tells that: the power delivered by the electric field is transferred with the same rate into other forms of energy. None of the energy can disappear.

As the unit of power is Watts [W] one can deduce that, in electricity, $1W=1V\times 1A$. Note that $1[J]=[W\times s]=[V\times A\times s]=1[V\times (C/s)\times s]=1V\times 1C$