Current and Resistance

Current and Resistance

What causes charges to flow, and what hinders the free flow of charge?
The most important practical applications of electrical phenomena are in the innumerable forms of electronic devices. In these, it is the motion of electrical charges that takes center stage. All materials contain huge numbers of both positive and negative electrical charges (in the form of protons and electrons comprising every atom of matter), and in most cases these charges are pretty much fixed in position – they don’t move around a lot. However in certain materials – for instance in metals – charged particles can move. (In metals it is the negative charges – the electrons – that actually move. We will however pretend that the moving charges are positive in order to simplify the discussion.) As noted in Chapter 4, these materials are called “conductors.”
In order to get the charges to start moving a force must act on them, and so an electric field must be present. You can imagine, as an example, a cylindrical piece of metal inside of which there is a uniform electric field, pointing along the length of the cylinder. If you stand at one fixed position in the cylinder and count the charges as they go past that point, you can measure the rate of flow of charge as a function of time. The term that is used to describe this rate of flow of charge is “current,” and the symbol for current is I. (The unit of current is the “ampere,” symbol “A.”) If an amount of charge equal to $\Delta q$ flows past a particular point in a time $\Delta t$ ,the current I is defined by this equation:
$CurrentI={\frac {\Delta q}{\Delta t}}$ 1ampere (1A) = 1 Coulomb/second

We will always assume that the flow of current is “steady,” that is, that the flow of charge continues without a stop and that the rate of flow does not change. In that case, will the number of charges that flow past line B every second be larger than, smaller than, or the same as the number that flow past line A every second?
Answer: the same. If fewer charges flow past line B than flow past line A, that would mean that some charges are getting “trapped” between lines A and B. If that continued long enough, something disastrous would happen – maybe the wire would explode! All those charges piling up in the same place would create a huge repulsive force that could not be contained. So this could not be a characteristic of “steady” flow of current.
On the other hand, if more charges flowed past line B than flow past line A, that would mean that some extra charges must be sneaking in to the wire somewhere between A and B. There would have to be some external source of charge besides the charges already present in the wire. This also is not a characteristic of “steady” flow of charge, and so it too can not happen. We say, then, that current is “conserved,” which means that the amount of charge flowing past any one point in the material is the same as that flowing past any other point, in a given amount of time. This will still hold true even if we place some obstacle in the path of the moving charges (for instance, some piece of material which offers more resistance to the flow of the charges). As long as the flow is steady, the current will be the same everywhere throughout any unbroken chain of conducting materials in direct contact with each other.
Now, we have just implied that some materials offer more “resistance” to the flow of charge than do other materials. (Materials that hinder the flow of charge are called “resistors.” The symbol for resistance is “R,” and it is measured in units called “ohms” [symbol: $\Omega$ ].) The reason is that in some materials, the charges – as they move – have a large number of collisions with the atoms in the material. In the course of these collisions, the charges lose some energy (which is transferred to the atoms of the material). ‘’Because of this continual loss of energy, the moving charges require a force provided by an electric field if they are to continue to flow.’’ Experiments show that the ‘’kinetic energy’’ of the flowing charges remains nearly constant; however, their total energy decreases as they flow through a resistor.
‘’Question’’: As charges flow through a resistor, does their potential energy increase, decrease, or remain the same?
‘’Answer’’: PE decreases. The energy lost by the flowing charges is transferred to the material of the resistor. As a result, the resistor will heat up, and may even give off light. At some point, the energy of the moving charges will have to be replenished if the flow of charge is to be “steady.” (We will see later on that this energy restoration process takes place when the charges flow through a battery.)
[What actually happens in the resistor is this: the electric force on the charges causes them to speed up briefly; however, before traveling more than a very tiny distance – less than 10–9 m – they collide with an atom and are slowed back down. During the collision, they transfer the energy they gained while speeding up to the atoms of the resistor. Then, this process is repeated trillions of times per second. The net result is that the average kinetic energy of the moving charges remains essentially constant. Their potential energy, and so their total energy, decreases, and there is a net transfer of energy from the moving charges, to the material of the resistor.]
Now, let’s think about how the amount of current flow through a resistor will be affected by the amount of resistance (a large resistance would correspond to a large value of “R”).
Question: All other things being equal, will increasing the value of R result in the amount of current flow increasing, decreasing, or remaining the same?
Answer: Decreasing. Actually, this is really a definition of resistance: more resistance means a bigger obstacle to current flow, so less current will flow (all other things being equal).
What about the relation between the amount of current flow, and the amount of PE lost by the charges as they flow through the resistor? Instead of discussing the potential energy, it is more convenient to refer to the change in electrical potential (i.e., PE per unit charge). Let us first decide whether the charges flow from high V to low V, or the other way around.
Question: As positive charges flow through a resistor, does their potential V increase, decrease, or remain the same?
Answer: Decrease. Since their PE decreases and V = PE/q, a smaller PE implies a smaller V (since q > 0).

Next, let’s consider the absolute value of the change in potential, Failed to parse (syntax error): {\displaystyle  \Delta V } .
We now have come to an extremely important point.
Question: Suppose we have two identical resistors – both with the same resistance R – and one of the resistors has a larger potential differenceV between its two ends. Will the amount of current flow through the resistor with the larger Failed to parse (syntax error): {\displaystyle  \Delta V } be larger, smaller, or the same as the amount of current flow through the resistor with the smaller Failed to parse (syntax error): {\displaystyle  \Delta V } ?
Hint: Consider the relative magnitude of the electrical force acting on the charges in each resistor.
Answer: Larger. As discussed previously, a larger Failed to parse (syntax error): {\displaystyle  \Delta V } implies a ‘’larger electric field magnitude E’’ (as long as the resistors are otherwise identical). A larger E means a larger magnitude of electrical force (since F = qE). This stronger force provides more “push” to the charges, and gives them a chance to speed up a bit more before they are slowed down again by a collision. Therefore, more charges per second are able to flow past a given point, and so the current I is larger. [Even though the charges are going slightly faster, the change in their average kinetic energy is still extremely small.]
We can put together our conclusions about the effect of resistance and potential difference on current flow in the form of a simple mathematical formula.
Question: Which of these equations is consistent with the behavior of current flow we have just discussed:
(A) $I=R\Delta V$

(B) $I={\frac {R}{\Delta V}}$  ;
(C) $I={\frac {\Delta V}{R}}$  ;
(D) $I={\frac {1}{R\Delta V}}$  ;
(E) I = constant [independent of R and V].
Answer: (C) I = V  R. This relationship is consistent with our expectations, since I increases when $\Delta V$

increases, but I decreases when R is larger. However, the exact proportionality between I and $\Delta V$ 

represented in this equation does not always hold for every material. It is true often enough, though, to be called “Ohm’s law.” It is often a very good approximation, and we will always assume that it is true for the systems that we examine.
Let’s look at an arrangement of two different resistors – R1 and R2 – connected by “perfectly conducting” wires. The arrow shows the direction of flow of current.
Question: Will the PE of the flowing charges at point B be larger, smaller, or the same as the PE of those same charges at point A? Answer: Smaller. The charges lose PE as they flow through a resistor. Question: Will the value of V at point B be larger, smaller, or the same as the value of V at point A?
Answer: Smaller. Since the PE of the positive charges is less at point B than at point A, the potential V must also be smaller at B.

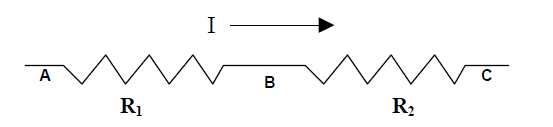
Now, lets use “ $\Delta PE_{AB}$ “ to symbolize the change in PE as the charges move from point A to point B, and “$\Delta PE_{BC}$” for the change as they move from B to C, etc.
Question: Will $\Delta PE_{AC}$ be larger, smaller, or equal to the quantity $[\Delta PE_{AB}+\Delta PE_{BC}]$ ?
Answer: Equal to. The total amount of potential energy lost by the charges during the full trip from A to C equals the sum of potential energy losses accumulated first from A to B, and then from B to C.