The Electric Field

Kreshnik Angoni and Kevin Lenton
Worksheet.docx
Worksheet.pdf
Additional Problems

Other Resources:

• Haliday & Resnick, Fundamentals of Physics 21.1-5
• Openstax
• Printable version

The Electric Field is an important extension of the Electric Force. The Electric Field allows you to describe the effect of charges on a point in space, without having to know what those source charges are, or what the distribution of charge is. In addition, if you know the Electric Field at any point, you can immediately calculate the force on any charge at that point.

Comparison with other Scalar and Vector Fields

If you use a very sensitive thermometer to measure the temperature at different locations in the city you will have a set of different values as a function of position. This distribution of temperature values in space is known as a temperature field. Similarly, a pressure field consists of a distribution of pressure values in different locations of atmosphere . In these two examples we deal with scalar fields because of the scalar nature of field parameter. The basic advantage of such kind of fields is the possibility to compare the values for a physical parameter at different space locations.
Similarly you can have a vector field, in which you can define the value and direction of the parameter at each point in space. Consider this diagram showing the wind vector field for the earth. The wind velocity is shown at each point with an arrow showing the direction and its length showing the value.

https://www.ncl.ucar.edu/Applications/Images/wind_3_lg.png
The electric field is a vector field. But how is the vector of the electric field defined ?

Definition of the Electric Field Vector E

Initially, the electric field definition appeared as an intermediary concept to answer questions: What way interact two electric charges? How do they know the presence of the other charge?

But when the electromagnetic theory was completed, the scientists understood that the electric field is not just an intermediary useful parameter; it is one of the basic constituents (matter and field) of the nature.

Nowadays, the following model of interaction between two electric charges is accepted: Once an electric charge Q is placed at a given point of space it creates its electric field at all space locations around it. Then, if another electric charge q appears at a point P of this space, it interacts straight away with the local electric field (created by the charge Q) at point P.

Definition: The electric field vector at a given point P of space is equal to the Coulomb force exerted on the unit positive charge (+1C) placed at point P.
In practice, one measures the force F exerted on a positive test charge qt (the test charge is very small, much less than 1C) and then finds out the electric field from the relation:
${\vec {E}}={\frac {\vec {F}}{q_{t}}}\qquad \qquad \qquad (1)$

Electric Field of a Point Charge

The electric field created by a point charge Q at the location r is defined by the expression
${\vec {E}}={\frac {\vec {F}}{q_{t}}}=k{\frac {q_{1}q_{t}}{r^{2}}}{\hat {r}}\cdot {\frac {1}{q_{t}}}=k{\frac {q}{r^{2}}}{\hat {r}}\qquad \qquad \qquad (2)$
where ${\vec {r}}=r{\hat {r}}$
Note: ${\hat {r}}$ is a unit vector in the direction of r. It simply means: in the direction of r

From Equation (1), it turns out that the SI unit of electric field is N/C.

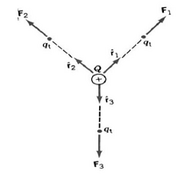
Fig 1. Shows how the Electric field can be found by considering the force on a test point charge at different locations of the space surrounding charge.

Equation (2) tells us that the electric field at a given point P of space depends on the location of P and the location of field source (that is to say the position of the charge producing the field). But, you can figure out that, for an electric charge q placed at P point, the electric field is defined at this location, no matter what charges produce it.
The force exerted on a charge q placed at point P can be found straight away from the local electric field EP as

${\vec {E}}=q\ {\vec {\vec {E_{P}}}}\qquad \qquad \qquad (3)$
If q > 0 (the charge is positive) the force has the same direction as the field and if q < 0 (the charge is positive) it has the opposite direction.
Since the principle of superposition is valid for Coulomb forces, it is valid for electric fields, too.
${\vec {E_{net}}}={\frac {\vec {F_{net}}}{q_{t}}}={\frac {\vec {F_{1}}}{q_{t}}}+{\frac {\vec {F_{2}}}{q_{t}}}+...{\frac {\vec {F_{N}}}{q_{t}}}={\vec {E_{1}}}+{\vec {E_{2}}}+...{\vec {E_{N}}}\qquad \qquad \qquad (4)$
That is to say you can add electric field vectors just like you can add electric force vectors.

ELECTRIC FIELD LINES

Field Lines are a way of visualizing the electric field produced by charge in a particular space.
Electric Field lines originate with positive charge and end with negative charge, as shown in the figure.

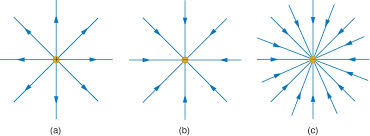
Let’s consider a positive charge +Q. The map of its electrical field in the surrounding space is shown in fig.2a. The electric field for a set of two equal charges +Q and +Q can be found as shown at fig.2b. If we draw the electric field at any point of space the picture becomes very complicated. So, you can use a system of field lines which helps to visualize the basic information on the field pattern.

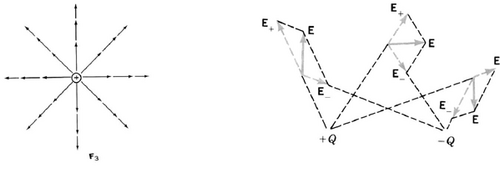
Fig. 2a Electric field map (+Q)
Fig.2b This shows how you could build up the Electric field map (+Q and -Q) by constructing the field contributions from each of the charges at any point. Field lines are a convenient way of plotting the results of this process.

Here are the rules of interpreting field lines and the resulting electric field vectors:

a) The electric field lines emerge from (+) charges and go towards (-) charges.

b) At any point, the direction of the electric field vector is tangential to the field line passing through the point in question.
c) The field lines never cross. Otherwise, it would mean there would be more than one direction for the vector of electric field at a given point!! (=not allowed)
d) The number of field lines around a space point (more precisely the field line density) is proportional to the magnitude of electric field at this point. Thus, the magnitude of electric field is large if the field lines are dense and small if the field lines are far apart.
e) While the electric field is a physical reality, the field lines are not. They are just an intermediary tool used to give quick visual and general information about the field.

Fig.3a The field lines for (+Q and –Q) Fig.3b The field lines for (+Q and +Q)
Electric dipole

Video Example 1 Courtesy of John Abbott College

Video Example 2 Courtesy of John Abbott College

CONTINUOUS CHARGE DISTRIBUTIONS

We have already seen how to calculate the electric field for a point charge. But most practical applications do not involved point charges, but continuous charge distributions. For instance, charge distributed on a line (=charge on a wire), and charge on a surface (e.g. = charge on a capacitor plate).
Remember that Coulomb’s law is valid for charged point particles. In order to find the electric field due to a continuous charge distribution, you must:

a) Divide the total charge into infinitesimal elements each of charge dq. i.e. consider the charge distribution as a sum of charges small enough that they look like point charges.

b) Apply the Coulomb’s law to each of these point-like charges and find the field due to each of them as
$d{\vec {E}}=k{\frac {dq}{r^{2}}}{\hat {r}}\qquad \qquad \qquad (8)$ c) Apply the principle of linear superposition and get the sum of all infinitesimal fields as

${\vec {E}}=\int _{chargedobject}d{\vec {E}}=k\ \int _{chargedobject}{\frac {dq}{r^{2}}}{\hat {r}}\qquad \qquad \qquad (9)$
Here it is important to remember that you have to always express dq as a function of location coordinates dq(x, y, z) so that you can calculate the value of the integral (9) practically.

Electric Field from an Infinite Line of Charge of Line Charge Density $\lambda$

Previous examples have involved point charges. In this example the charge distribution is continuous.
Recall that for a system of charges you calculate the net electric field by taking the vector sum of all the contributions (principle of superposition). For a continuous charge distribution the sum becomes an integral over all the contributions.
You can describe the charge distribution using the line charge density $\lambda$. Where $Q_{total}=\lambda _{total}\times Length$.

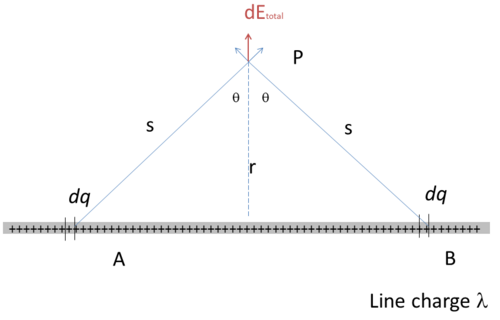
First consider the electric field due to a small segment A of the line of charge to the left of P. The magnitude of this field is given by Coulomb’s law, and the direction of the field points directly away from the segment. Next, consider the electric field due to a small segment B, of the line of charge to the right of P. The magnitude of the electric field from segment B is the same as the magnitude of the electric field from A since A and B are equidistant from point P. However, the electric field from B has a negative x component that exactly cancels the positive x component of the electric field from A.
As we integrate from $-\infty$ to $+\infty$ you can see that for every segment of the line to the left of P there is another segment of the line to the right of P whose x component of the field exactly cancels the x-component from the initial segment, just as we saw for A and B. Consequently the total field at point P must point in the y direction.
To calculate the magnitude of the net field at P, we begin by writing an expression for the y component of the electric field due to a small segment of the charges line that we can treat as a point source. The magnitude dE of the electric field due to this segment is proportional to the amount of charge in the segment dq and is inversely proportional to s^2, the square of the distance from P.
$dE=k{\frac {dq}{s^{2}}}$

To find the total field, we will only need to consider the y component: $dE=k{\frac {dq}{s^{2}}}cos\theta$

Because both the distance s and the angle change with x, you should rewrite the integral in terms of one variable. Let’s choose $\theta$!
Use:
$s={\frac {r}{cos\theta }}$ and $x=rtan\theta$
Take the derivative of this last equation to yield $dx={\frac {r}{cos^{2}\theta }}d\theta$
The equation for the net electric field then becomes:
$E=\int dE_{y}=\int _{-\pi /2}^{+\pi /2}k{\frac {\lambda }{r}}cos\theta d\theta =2k{\frac {\lambda }{r}}$

$E=2k{\frac {\lambda }{r}}$  

Phew!
The good news is you do not need to know this proof, although you need to know that the electric field from an infinite line charge is equal to $E_{infinitelinecharge}=2k{\frac {\lambda }{r}}$ and is always perpendicular from the wire.
However the proof shows some principles that you will use in future:
1. The physical meaning of integration is the summation of elements (in this case all the dE s). You are using the principle of superposition here.
2. You can use symmetry as a way of simplifying the problem In this case realizing that the x components cancel out. This only happens when you have an infinite line charge, non-infinite makes it a bit more complicated. Note that any line charge looks infinite if you are close enough to it.

Want more?
Consult these video explanations:
Electric Field of a finite line charge Video 1; Video 2
Electric Field of a ring of charge

The Electric Field of an Infinite Plane of Charge

http://physics-help.info/physicsguide/electricity/gauss_law_images/image030.gif
This Figure shows part of an infinitely large, and very thin, conducting plane with a uniform distribution of charge. The electric field vector at any point of space in either side of this sheet is perpendicular to the sheet plane because the parallel components wipe out each other. A closer consideration shows that the magnitude of its electric field is the same in the surrounding space. If the vector E is the same at every point of space, the field is called a uniform electric field.
The electric field of an infinite plane of charge is defined by:

${\vec {E}}_{infiniteplane}={\frac {\sigma }{2\varepsilon _{0}}}\qquad \qquad \qquad (5)$

Where
$\sigma$ is the area charge density. $\sigma ={\frac {Total\ Charge}{Total\ Area}}$ Units: C/m^2
$\varepsilon _{0}$ is the permittivity of free space $\varepsilon _{0}=8.854\times 10^{-12}[F/m]$. Note that $k={\frac {1}{4\pi \varepsilon _{0}}}$
Note:
The field is:

• Constant to infinity
• Perpendicular to both surfaces
• Proportional to the charge density
• For a negative charge density, the E field goes into the plane, not away from.

The E Field inside a Conductor is Zero

When a neutral homogeneous conductor is placed inside an external electric field ${\vec {E}}_{ext}$ , its free electrons move quickly in the opposite direction of ${\vec {E}}_{ext}$ (Fig.5a) [because the electrons are negative] and leave an unbalanced positive charge on the other side. This charge redistribution inside the conductor creates an internal field ${\vec {E}}_{int}$ that is directed in the opposite direction to ${\vec {E}}_{ext}$ . As long as ${\vec {E}}_{total}$ is not equal to zero, the electrons continue to move in a way that increases the magnitude of ${\vec {E}}_{int}$ and consequently decreases the magnitude of the total E filed inside; when ${\vec {E}}_{total}=0$ they stop moving. So, under static conditions, the net macroscopic field inside a homogeneous conductor is zero.
This is to say inside a conductor, the static E field is zero because if it were not zero, charge would move, until it is zero, and the situation would not be static.
Another consequence of this is that the free charge always accumulates on the outside of a conductor. The charge moves until it cannot move anymore, i.e. the outside edge of the object.
Take note that this is not true for insulators, because the charge is not free to move.

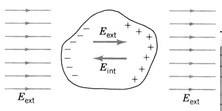
Figure 5a: Showing how charge moves in a conductor such that the electric field inside is always equal to zero.

Electric Field Close to the Surface of a Conductor

The easiest way to look at the field close to the surface of a conductor is to get infinitely close to that surface. If you get infinitely close then what you see is actually a flat infinite surface of charge. Therefore the electric field will always be perpendicular to the surface! And the magnitude very close to the surface is given by equation (5)
Note that this approximation is true even for curved surface, because even a curved surface is flat if you are infinitely close to it. We are in the realm of classical physics, where you can get infinitely close, not considering atoms and all that modern physics malarky.

Another way of looking at it is that like charge pushes all other like charge away from it. Therefore the charges will distribute themselves on the surface such that they cannot move sideways anymore, that is to say the net force (and therefore net E field) parallel to the surface is zero.

Remember the field inside a conductor is zero, and the field just outside a conductor is always perpendicular and proportional to the charge density at that point.

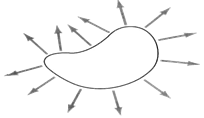
Figure 5b: Showing how the electric field just outide a conductor is always perpendicular to the surface.

MOTION OF CHARGES IN UNIFORM FIELDS

If a free charged particle (such as an electron or a free proton) is moving inside a static uniform electric field it is subjected to the electric force with magnitude
$|{\vec {F}}_{electric}|=|q{\vec {E}}|\qquad \qquad \qquad (6)$

Due to their small mass, in general, the gravitation force on elementary particle is much smaller than electric force, and is usually ignored.
So, it turns out that the net force exerted on particle is equal to the electric force.
In these circumstances, the Newton’s second law gives

$\sum {\vec {F}}={\vec {F}}_{electric}=m{\vec {a}}\qquad \qquad \qquad (7)$
and the particle moves with a constant acceleration (E is constant if the field is uniform).

${\vec {a}}={\frac {q{\vec {E}}}{m}}\qquad \qquad \qquad (8)$

Note that the electric field gives the direction of the force, and therefore the acceleration only. If the particle has a velocity, it will not follow the electric field lines. Rather, the acceleration vector will be in the same direction as the field lines.
In general you only have to consider the motion of charge in uniform electric fields (e.g. produced by an infinite plane of charge). Therefore you have a force and acceleration in only one direction = parabolic motion!!.
Review your kinematic formulas.

Examples

1. Electric Field of Point Charges
Two charges are held fixed on a horizontal plane: q1(1.00μC) is at (-1,3)cm and q2 (-2μC) is at the origin.
Find the net electric field at point P3 (2,1)cm.

2. Motion of a charged particle in an electric field
In a poorly aligned cathode ray tube, electrons enter a vertical uniform electric field with a velocity of 5x10^7 m/s at 20 deg above the horizontal.
The electrons hit the top plate, 1.00 cm up and 2.00cm to the right from the place where they entered the electric field.
What is the magnitude of the electric field, and in which direction does it point?