Module 3b: Area under Kinematic Graphs

You have already seen how to find instantaneous velocity from a graph of x vs. t and acceleration from a graph of v vs. t by using the slopes ( ${\frac {dx}{dt}};{\frac {dv}{dt}}$ ) of tangents on the graph at points of interest. The following “inverse” situations happen in practice, too:
a) Given the graph v vs.t find the location of particle x at a given moment t.
b) Given the graph a vs. t, find the velocity of particle v at a given moment t.

Finding the Area Under a Curve

Finding the location of particle at time t_2 from the velocity graph

Knowing that $v={\frac {dx}{dt}}$
(1) is a mathematical definition, while in physics, one deals with measurable (small but finite) interval values $\Delta x,\Delta t$, one uses $v={\frac {\Delta x}{\Delta t}}$,
(2) for a real life velocity and $\Delta x=v\times \Delta t$, (distance=speed times time)
(3) For a motion with constant velocity (graph in fig. 1) one may calculate the displacement from initial location $x_{1}att_{1}as\Delta x=x_{f}-x_{i}=v\times \Delta t=v\times (t_{f}-t_{i})$ (3)
As $v\times (t_{f}-t_{i})$ is the area of rectangle (fig.1), the displacement is equal to the area under the velocity graph for the considered time interval. ($v\times (t_{f}-t_{i})$ has displacement dimensions [m/s]*[s]=[m])

The result “displacement $\Delta x=x_{f}-x_{i}$ equal to area under velocity graph” is valid in all cases but the way one calculates the area is more subtlet if the velocity is not constant (fig.2). One has to calculate the area by using a set of ‘’extremely’’ narrow rectangles covering the area under the graph as much as possible. You can probably tell that this method is more precise when using tiny time intervals $\Delta t$.
The figures 3,4 show two possible velocity graphs. As the area under the graph in fig.3 is a positive value, it meand that $\Delta x=x_{f}-x_{i}>0$ (the displacement is positive)and $x_{f}>x_{i}$ . This means that the particle is moving along the positive x axis. In fig. 4, the area under the graph is negative, so we have $\Delta x=x_{f}-x_{i}<0$ and $x_{f}<x_{i}$. This means that the particle is moving along the negative x axis.

B] Finding the velocity of particle at the “moment t2 “ from the acceleration vs t graph
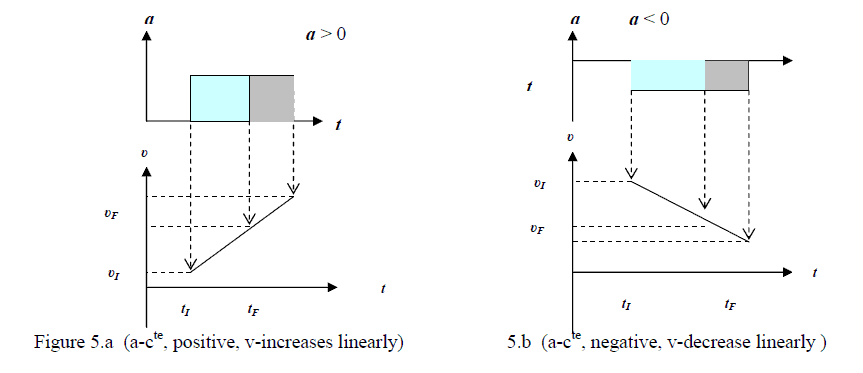
Similarly, if one has an a vs t graph, one may calculate the change of particle velocity by the area under the graph. In the frequent case of motion with constant acceleration (figure 5.a,b), one may easily calculate the velocity at any moment (F-final) if one knows it at an initial (I) moment of time.
The definition for acceleration is $a={\frac {\Delta v}{\Delta t}}$ (4) As “a” is constant one can express it by “initial and final values” $a={\frac {v_{f}-v_{i}}{t_{f}-t_{i}}}$ (5) So, $v_{f}-v_{i}=a\times (t_{f}-t_{i})$ (6) The time interval being positive, a-sign shows if the velocity value2 increases (5.a) or decreases (5.b).

Even when “a” is not constant, the area under the a(t) graph gives the change of velocity but in these cases the velocity does not change linearly with time (Ex. we will see later at “harmonic oscillations”).