Conservation of Energy EX 2

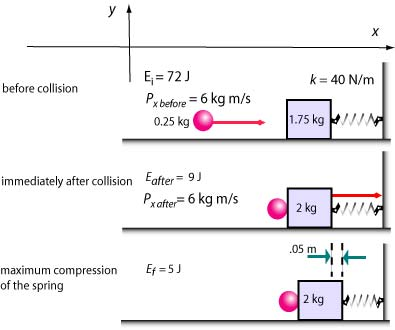
In this problem, the system is the projectile-block-spring-Earth. First, there is a completely inelastic collision between the projectile and the block. We know that a system loses energy during an inelastic collision. Then, the block with the projectile sticking to it moves along the rough surface while the system loses energy because of the work done on the system by friction, a non-conservative force. When the spring compression is at its maximum, the block is at rest. Therefore at the end, all of the system's energy ($E_{f}$) is in the spring potential energy. The initial compression of the spring is zero and the final compression is 0.5 m, so we can compute

$E_{f}={\frac {1}{2}}kx^{2}={\frac {1}{2}}(40)(0.5)^{2}=5J$

We can easily determine the energy of the system before the collision because all of the system's energy ($E_{i}$) is in the kinetic energy for the projectile of mass $m_{p}=0.25kg$ and velocity $v_{p}=24m/s$.

$E_{i}={\frac {1}{2}}m_{p}{v_{p}}^{2}={\frac {1}{2}}(0.25)(24)^{2}=72J$

Now we have to account for the losses. The system first loses energy in the collision. The momentum is conserved in the collision but the kinetic energy is not. We will use the law of conservation of momentum to determine the speed of the block with the projectile sticking to it. Let's choose the coordinate system with the x-axis pointing towards the right. The x-component of the momentum before the collision is equal to the momentum of the projectile.

${P_{before}}_{x}=m_{p}v_{p}=(0.25)(24)=6kgm/s$

Since the momentum after the collision is the same and since the two masses ($m_{pb}=0.25+1.75=2kg$) stick together, we can write the momentum after the collision:

${P_{after}}_{x}=m_{pb}v=2v=6kgm/s$

where $v$ is the speed of the block with the projectile sticking to it. Solving this equation for $v$, we find $v=3m/s$. Consequently, the kinetic energy of the system after the collision is

$K_{after}={\frac {1}{2}}mv^{2}={\frac {1}{2}}(2)(3)^{2}=9J$

Since right after the collision (while the spring is still uncompressed) the total energy of the system is still in the form of kinetic energy of the block with the projectile sticking to it and is now $E=9J$, then the change in the system's energy was -63 J during the collision.

Just before the block begins the slide (just after the collision) the energy of the system is 9 J. Since the final energy of the system is 5 J we conclude that the work done by friction while the block slides is equal to the change in energy during this interal of time. We use the equation

$\Delta E=W_{NC}$

$\Delta E=5-9=-4J=W_{F_{f}}$

The displacement is equal to the maximum compression of the spring $\Delta r=0.5m$. The force of kinetic friction is opposite the direction of motion ($\theta$ = 180°) and consequently, we may write

$W_{F_{f}}=F_{f}\Delta r\cos {\theta }=F_{f}(0.5)(-1)=-0.5F_{f}=-4J$

Solving for $F_{f}$, we find

$F_{f}=8N$

Note that the gravitational potential energy does not change because the movement is along the horizontal.