Static Equilibrium EX 2
We will think of the forearm as a rod of length 0.3 m. It pulls the rope with a force of 50 N downward so the tension in the rope exerts an upward force of 50 N on the forearm (Third Law). The weight of the forearm, , is 20 N, and acts downward at the centre of mass. The force is exerted by the tricep muscle that pulls on the forearm upward. The forearm is in static equilibrium so the net force is equal to zero. Now note the following "problem": assuming the y-axis points upward, we can write
which gives . This result does not make sense because triceps can only contract and pull. By the way, all muscles pull by contracting. The y-component of the force exerted by the triceps should be positive given the position at which is attached to the bone. We re-examine the situation, and realize that the forearm is in contact with the bones in the upper arm at the elbow joint which is also a pivot about which the lower arm rotates. The only explanation, then, is that the bones in the upper arm exert a downward force on the forearm. The diagram below summarizes all forces acting on the forearm.
The diagram also shows the lever arm of each of these forces. Note that the tricep acts at a distance 1.2 cm (0.012 m) from the pivot. The gravitational force acts at the centre of mass, that is, at a distance 0.30/2 - 0.012 = 0.138 m from the pivot. The tension in the rope pulls the arm at a distance 0.30 - 0.012 = 0.288 m from the pivot. The forcevectors and the associated lever arm vectors are colour coded for easy identification.
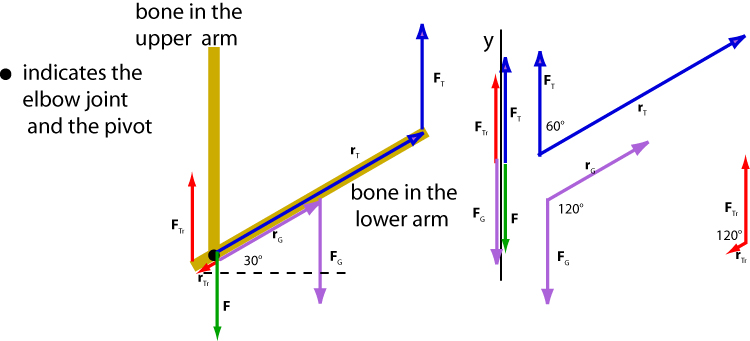
Using Newton's Second Law for the y-component we get
We cannot solve this equation directly, so we turn our attention to the torques exerted by these forces. We will only show the Method 1 in this solution.
| Forces | Direction | Torque |
|---|---|---|
| CCW | ||
| CW | ||
| CW | ||
| 0 |
Solving the equation we obtain
Substituting this value in the equation for y-components of forces we obtain
Note the enormity of forces exerted by the muscle and on the joint. The fact is that our body was not developed to be "strong". We are built so that we can move fast. This particular attribute of our physique probably protected our species more efficiently from extinction.