Static Equilibrium EX 1
To solve this problem we will assume that the tension in the cable is 1000 N. We will begin with forces exerted on the boom: the weight of the boom acts at the center of the mass 2 m from the pivot; the load is a force acting downward (it is really tension in the wire from which the load is suspended) and it acts at a distance 4 m from the pivot; the tension acts at a distance 3 m from the pivot; and finally, the force exerted on the boom by the hinge is broken in the diagram below into two components and . Since the boom is in equilibrium we are free to choose the axis as shown in the diagram. Note that we have colour coded each force and its arm lever.
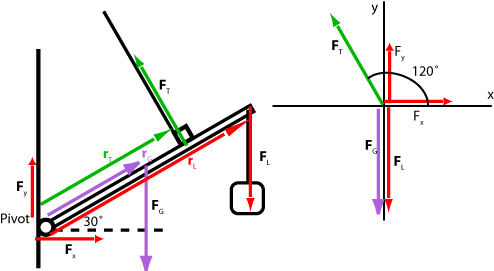
The boom is in equilibrium and therefore
We will begin by computing the components of each of the forces:
| Forces | x-component | y-component |
|---|---|---|
| 0 | -200 N | |
| 0 | ||
| 1000 cos(120°) = -500 N | 1000 sin(120°) = 867 N | |
| 0 | 0 |
We can solve the equation for the x-components and write
but we cannot solve the equation for the vertical components of the forces. We need to compute the torques and then use the fact that the net torque is zero.
To compute the torques we will show all three methods and you choose which one seems to be easier to use:

The torque exerted by the force is zero because the force acts at the pivot. The three methods are identical for the torque exerted by the tension since the tension is perpendicular to its lever arm. The torque exerted by the tension is positive since it is counterclockwise. The torque exerted by and is negative because it is clockwise.
| Forces | Method 1 | Method 2 | Method 3 |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 0 | 0 |
Solving the equation we find
Then we can solve the equation for the y-components to find
The negative sign indicates that the vertical component of the force exerted by the hinge on the boom points downward. Given the third Newton Law, the force exerted by the boom on the hinge is opposite to the force exerted by the hinge on the boom and so we can write that