Newton's 3rd Law EX 4

First we will picture the problem situation and think about the forces involved in this problem. Once we have a clearer understanding of what may happen we will attempt to answer the questions. We will begin by drawing a picture.

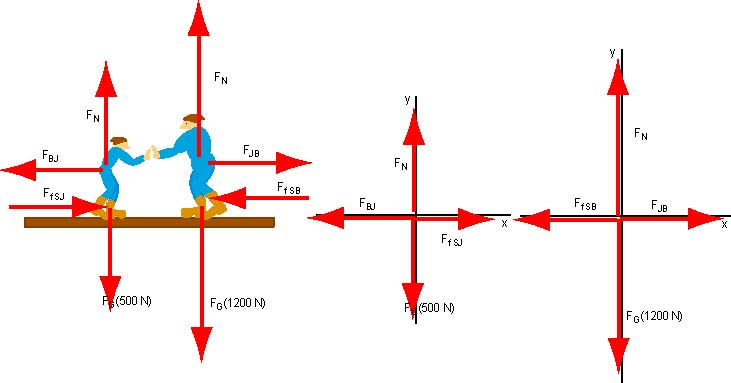
Then we list the forces and draw free body diagrams for both Jim and Bob.

Note that in these diagrams we have taken into account the magnitude of their weight. Because we are picturing them on a horizontal surface, the magnitude of the normal force is equal to the magnitude of their weight. The maximum force of friction exerted on Jim is $F_{f}=250$ N. Similarly the maximum force of friction exerted on Bob is $F_{f}=600$ N. According to the third Newton's Law, $F_{JB}=F_{BJ}$ (note that we are referring to the magnitude of these two forces; their direction is indicated in the above diagram). Let us examine a few situations which may arise. For example, Jim pushes Bob with a force of 100 N. Then Bob will push back with a force of 100 N. Since the external force on Jim is less then the maximum force of friction Jim will remain at rest. Similarly, Bob is at rest for similar reasons. Note that in this case the force of friction on both, Bob and Jim is the same.

Suppose that Jim pushes Bob with a force of 300 N. Then Bob exerts 300 N on Jim. The external force on Jim exceeds the maximum force of friction that he can experience and the net force on Jim is 50 N pointing to the left. Jim will slip (accelerate) to the left. This situation is similar to situations you have probably experienced on a number of occasions: for example when trying to move a very heavy piece of furniture or pushing your car stuck in the snow. You may recall that you pushed as hard as you could and your feet began to slip backward. Consequently, you had to push less. Similarly, it is unlikely that Jim would attempt to push Bob with a force exceeding 300 N. In contrast, Bob does not accelerate because the external force on him is below the maximum force of friction that he can experience. Consequently, the force of friction on him is 300 N and he remains at rest. Note that here the force of friction exerted on Jim is smaller than the force of friction exerted on Bob.

Suppose that Bob pushes Jim with a force of 400 N. Then according to "THE LAW" Jim exerts the force of 400 N on Bob and the force of friction exerted on Bob balances the force exerted by Jim. Consequently, Bob remains at rest. Jim on the other hand accelerates to the left because the net force on him is 150 N pointing to the left and thus the magnitude of acceleration is $a={150 \over 50}=3m/s^{2}$. We may conclude that it does not matter who initiates the push: the force exerted by Bob on Jim ($F_{JB}$}) is equal to the force exerted by Jim on Bob ($F_{BJ}$}). This is "THE LAW". We also conclude that both of these forces are likely to be larger when Bob initiates the push. Jim knowing that he is likely to slip will probably tend to initiate a push which is smaller than or equal to 250 N. Bob on the other hand knows that he can initiate the push up to 600 N without slipping.

Now we are ready to answer the questions:

(a) According to Newton's Third Law, these two forces are equal in magnitude.

(b) Not necessarily. When neither of them accelerate (a gentle push) the force of friction may be the same.

(c) It is true according to the third Newton Law.

(d) This statement is incorrect. A force that can balance the force exerted by Jim on Bob must be exerted on Bob.

(e) Yes this is true. When the force exerted on Jim by Bob is smaller or equal to the maximum force of static friction on Jim, then the two forces cancel out and Jim stays at rest.