Newtons Laws EX 37

The two masses are placed on the x-axis as shown in the diagram below:

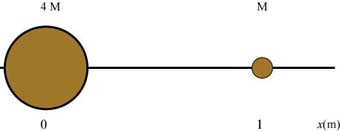
Now, we want to place the small particle of mass $m$ so that it is in equilibrium. There are only two forces acting on this particle: the gravitational force exerted by the mass $4M$, $F_{G_{4}}$, and the gravitational force exerted by the mass $M$, $F_{G}$. Both of these forces are attractive. In other words, $F_{G_{4}}$ points towards the mass $4M$ and $F_{G}$ points towards the mass $M$. Since we want $m$ to be in equilibrium we are looking for a place where these two forces have equal magnitudes and opposite directions.

Let's think where we could place the particle $m$ so that the forces have equal magnitudes and opposite directions. We can think of three regions in the space around the masses $4M$ and $M$ (see the diagram below): x-axis, the gray region above and greenish region below the x-axis.

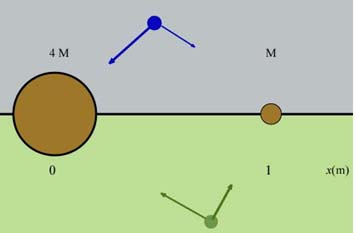
As you can see from the sketches above, the placement of $m$ in either the blue or greenish region results in forces which do not have opposite directions. Therefore we should look for a placement along the x-axis. Try to visualize which way the two forces will act if the particle $m$ is (i) to the left of $4M$, (ii) in between the two masses, and (iii) to the right of mass $M$. I think that you will reach the conclusion that the particle $m$ should be located between $4M$ and $M$ at some distance $x$ from $4M$. Its distance from $M$ will then be (1 - x).

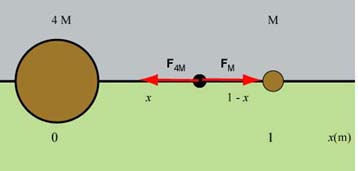
Now we can use the Newton Law of gravitation and write the equation stating that the magnitudes of the two forces are equal:

$F_{G_{4}}=F_{G}$

${G(4M)m \over x^{2}}={G(M)m \over (1-x)^{2}}$

Cancelling $G$, $M$ and $m$, we get:

${4 \over x^{2}}={1 \over (1-x)^{2}}$

Take (positive) square roots:

${2 \over x}={1 \over 1-x}$

Cross multiply and solve for $x$ to find $x=2/3$ m.