Proj Motion EX 1
Helena Dedic
An object is launched from the ground at some angle above horizontal. Three seconds later, its velocity v is (20 m/s, -4 m/s). Find how far (horizontally) and how high the object will fly.
Solution:
We choose coordinate system with origin at the point where the object is launched and the positive y-axis pointing upward.
Since the object was launched at some angle above horizontal, both the x and y-components of initial velocity are positive.
The x-component of velocity remains constant throughout free fall.
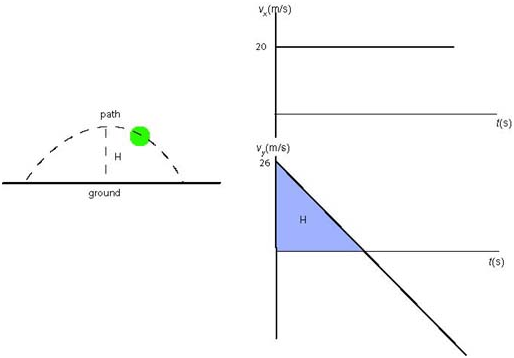
We are given the components of the velocity at t = 3 s, where, again, in particular, the x-component, 20 m/s, remains the same from launch to landing.
Thus the graph of is a flat line crossing the at 20.
The y-component of velocity is initially positive and it decreases at a rate of 10 m/s every second. Thus in three seconds the y-component of velocity decreases by 30 m/s.
Given that at t = 3 s the y-component of velocity was -4 m/s, we deduce the object was launched with initial y-component of velocity equal to 26 m/s.
At t = 3 s, the object was already on its way down. We are now ready to draw velocity graphs:
How high will it have flown? To this end, we need to figure out where the y-component of velocity is zero.
Given that it decreases 10 m/s every second we deduce that vy = 0 at t = 2.6 s; and the maximum height H is equal to the area of the blue triangle (i.e., the corresponding area under the graph); namely, H = ½ × 26 × 2.6 = 33.8 m.
Note the path is symmetrical, because the object lands at the same height it was launched. The time to go up is the same as the time to get back down (acceleration is constant). Consequently, the object will have landed in 5.2 s and during this time it will have travelled a horizontal distance of 5.2 × 20 = 104 m.